Wahrscheinlichkeit 
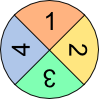
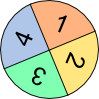
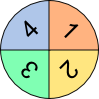
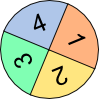
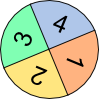
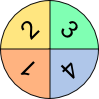
Aufgabe 1: Der Computer vergößert zufällig eines der abgebildeten Glückssymbole. Die Wahrscheinlichkeit zu erscheinen, ist im entsprechenden Klappfeld angegeben. Warum ist es unwahrscheinlich, dass bei einer Wahrscheinlichkeit von 1 5 nach 5-maligem Klick auf "Neu" bereits alle 5 Symbole erschienen sind?
Wahrscheinlichkeit: Klicks: 0 |
 |
Aufgabe 2: Klick die richtigen Begriffe an.
|
Versuche: 0
Aufgabe 3: Klick die richtigen Vergleichszeichen zwischen den Wahrscheinlichkeiten an.
| a) |
|
|
b) |
|
|
c) |
|
|
|||||||||||||||
| d) |
|
|
e) |
|
|
f) |
|
|
Versuche: 0
Aufgabe 4: Gib die aufgeführten Wahrscheinlichkeiten in Prozent an.
| a) | 1 | = % b) | 1 | = % c) | 1 | = % d) | 1 | = % |
| 2 | 5 | 4 | 20 |
Versuche: 0
Aufgabe 5: Trage die richtige Prozentangabe zum Bruch ein.
| 1 | = % |
| 2 |
richtig: 0falsch: 0
Aufgabe 6: Klick die richtigen Vergleichszeichen zwischen den Wahrscheinlichkeiten an.
| a) 0,45 | 1 | b) 0,33 | 0,040 | c) 33 % | 1 | |||
| 2 |
3 |
| d) | 1 | 50 % | e) | 3 |
4 | f) | 1 | 99 % | |||
| 2 | 4 |
5 |
Versuche: 0
Einstufige Zufallsversuche
Beim Wurf eines sechsseitigen Würfels liegt die Wahrscheinlichkeit, eine 2 zu werfen bei 1 6 . Ebenso liegt die Wahrscheinlichkeit eine 3 zu werfen bei 1 6 . Wie groß aber ist die Wahrscheinlichkeit, ein 2 oder eine 3 zu würfeln? Sie liegt bei 1 6 + 1 6 = 2 6 = 1 3 Besteht ein Ereignis aus mehreren Ergebnissen, so werden die Wahrscheinlichkeiten der Einzelergebnisse addiert.
| Wahrscheinlichkeit = | Anzahl der günstigen Ergebnisse |
| Anzahl der möglichen Ergebnisse |
Aufgabe 7: Bestimme die Wahrscheinlichkeit für folgende Ereignisse.
| Ereignis | Anzahl der günstigen Ergebnisse |
Anzahl der möglichen Ergebnisse |
Wahrscheinlichkeit | ||
| Mit dem Würfel eine 6 zu werfen |
|
||||
| Mit dem Würfel eine durch 3 teilbare Zahl zu werfen |
|
||||
| Mit dem Würfel eine gerade Zahl zu werfen |
|
||||
| Drehen einer Primzahl bei einem Glücksrad mit den Zahlen 1 bis 16 |
|
Versuche: 0
Aufgabe 8: Wie wahrscheinlich ist es, mit einem 10-seitigen Würfel a) eine 9 und b) eine kleinere Zahl als 4 zu würfeln?

a) Die Wahrscheinlichkeit eine 9 zu würfeln liegt bei %.
|
||||||
Versuche: 0
Aufgabe 9: Mit welcher Wahrscheinlichkeit sagt die folgende Bauernregel das Wetter richtig voraus?
Wenn der Hahn kräht auf dem Mist, ändert sich das Wetter oder es bleibt, wie es ist.

Die Regel sagt mit einer Wahrscheinlichkeit von % das Wetter richtig voraus.
Versuche: 0
Aufgabe 10: In einem Beutel befinden sich zwei rote und drei grüne Kugeln. Wie viele Kugeln müssen aus dem Beutel gezogen werden, um ganz sicher von jeder Farbe mindesten eine Kugel zu haben?

Um ganz sicher zu sein, müssen Kugeln gezogen werden.
Versuche: 0
Aufgabe 11: In einem Gefäß befinden sich 100 Kugeln. Wie viele Kugeln müssen grün sein, damit die aufgeführte Wahrscheinlichkeit, eine grüne Kugel zu ziehen, stimmt?
| a) 10 % = Kugeln | b) 1 4 = Kugeln |
| c) 15 % = Kugeln | d) 3 10 = Kugeln |
| e) 27 % = Kugeln | f) 2 5 = Kugeln |
Versuche: 0
Aufgabe 12: Trage die Wahrscheinlichkeit ein, mit der aus den abgebildeten Säcken die rote Kugel herausgezogen wird.
a) |
b) |
c) |
d) |
|||||||||
| als gekürzter Bruch |
|
|
|
|
||||||||
| in Prozent | % | % | % | % |
Versuche: 0
Aufgabe 13: Aus dem Behälter wird eine rote und eine orange Kugel gezogen und weggelegt. Mit welcher Wahrscheinlichkeit ist die nächste gezogenen Kugel blau?

Die Wahrscheinlichkeit beträgt %.
Versuche: 0
Aufgabe 14: Zwei 50-Cent-Münzen werden in die Luft geworfen. Mit welcher Wahrscheinlichkeit landen die unten aufgeführten Kombinationen auf dem Boden?
Wurfkombinationen |
||||||||
| A | B | C | D | |||||
| Münze 1 |  |
 |
 |
 |
||||
| Münze 2 |  |
 |
 |
 |
||||
| a) Zweimal Zahl? |
|
||
| b) Einmal Zahl und einmal Tor? |
|
||
| c) Zweimal Tor? |
|
Versuche: 0
Aufgabe 15: Aus den drei farbigen Holzringen sollen unterschiedlich farbige Türme gebaut werden.
- a) Wie viele Möglichkeiten gibt es, die Türme anzuordnen?
- b) Wie wahrscheinlich ist es, dass die rote Scheibe in der Mitte liegt?

| a) | Es können verschiedene Türme hergestellt werden. | ||||
| b) |
|
Versuche: 0
Aufgabe 16: Gina stellt mit den beiden Zahlenprismen eine Zahl ein, ohne hinzuschauen. Mit welcher Wahrscheinlichkeit entsteht eine zweistellige, gerade Zahl?
Die Wahrscheinlichkeit liegt bei %.
Versuche: 0
Aufgabe 17: Adrian stellt mit den beiden Zahlenprismen eine Zahl ein, ohne hinzuschauen. Mit welcher Wahrscheinlichkeit entsteht eine zweistellige, gerade Zahl?
Die Wahrscheinlichkeit liegt bei %.
Versuche: 0
Aufgabe 18: Gib die Wahrscheinlichkeit des Ergebnisses an.
| Wie hoch ist die Wahrscheinlichkeit ... | Antwort | |||
| a) eine Fünf als letzte Ziffer der Telefonnummer zu haben? |
| |||
| b) an einem Sonntag Geburtstag zu haben? |
| |||
| c) nach dem Werfen einer Münze die Zahlseite zu sehen? |
| |||
| d) von 5 Äpfeln, den einen mit dem Wurm zu nehmen? | % | |||
| e) mit einem Würfel eine ungerade Zahl zu werfen? | % | |||
Versuche: 0
Aufgabe 19: Wie wahrscheinlich ist es beim folgenden "Mensch-ärgere-dich-nicht-Spiel, dass
| a) | die blaue Figur eine rote Figur herauswirft? |
| b) | eine rote Figur mit einem Wurf die gelbe Figur herauswirft? |
| c) | die grüne Figur ins Ziel kommt? |

Mit folgenden Wahrscheinlichkeiten treten die Ereignisse ein:
| a) | 1 | b) | 1 | c) | 1 |
Versuche: 0
Aufgabe 20: Betrachte das Glücksrad.

| a) | Mit welcher Wahrscheinlichkeit bleibt das Glücksrad auf dem roten Feld stehen? |
| b) | Wie groß ist die Wahrscheinlichkeit, dass das Glücksrad auf einem der gelben Felder stehen bleibt? |
| c) | Frank wählt die lilafarbigen und Hanna die blauen Felder. Wer hat die größere Gewinnchance? |
| d) | Welche Farbe bietet die größte Gewinnchance? |
| Antworten: | |||||
| a) | 1 | b) | 1 | c) | d) |
Versuche: 0
Aufgabe 21: Gib als gekürzten Bruch und in Prozentschreibweise die Wahrscheinlichkeit an, mit der beim Glücksrad ein Feld gewinnt.

| Die Wahrscheinlichkeit liegt bei | . Also bei % | |
richtig: 0falsch: 0
Aufgabe 22: Bei einem Glücksrad sind alle Flächen gleich groß und haben eine unterschiedliche Farbe. Vervollständige die Sätze richtig.
- Je weniger Flächen vorhanden sind, umso ist die Wahrscheinlichkeit, auf einer vorgegebenen Farbe stehen zu bleiben.
- Jede Farbe kann mit Wahrscheinlichkeit gedreht werden.
- Wenn die Wahrscheinlichkeit, eine Farbe zu drehen bei 5% liegt, dann ist das Glücksrad in Flächen unterteilt. Jede Fläche hat einen Winkel von °.
- Bei einer Farbe, die bereits gedreht wurde, ist die Wahrscheinlichkeit daraufhin nochmals gedreht zu werden.
Versuche: 0
Aufgabe 23: Wie groß ist die Wahrscheinlichkeit, mit dem folgenden Glückskreisel a) eine 3 und b) ein blaues Feld zu drehen?

|
Versuche: 0
Aufgabe 24: Wie groß ist beim unteren Glücksrad die Wahrscheinlichkeit:
|
a) eine 5 zu erzielen? b) kein oranges Feld zu treffen? c) ein blaues Feld zu erreichen? d) eine gelbe 4 zu drehen? e) ein grünes Feld zu treffen? f) eine ungerade Zahl zu erzielen? |

|
|||||||||||||||||||||||||
Trage als Antwort den gekürzten Bruch ein.
|
||||||||||||||||||||||||||
Versuche: 0
Aufgabe 25: Das Glücksrad wird ein Mal gedreht. Trage unten die richtigen Wahrscheinlichkeiten für die angegebenen Zahlen als gekürzten Bruch und in Prozent ein.
|
||||||||
|
als gekürzter Bruch |
in Prozent |
|||||||
| a) eine Zahl ≥ 3 | % | |||||||
| b) eine Zahl > 3 | % | |||||||
| c) eine gerade Zahl | % | |||||||
| d) eine ungerade Zahl < 3 | % | |||||||
Versuche: 0
Aufgabe 26: Das Glücksrad wird ein Mal gedreht. Trage unten die richtigen Wahrscheinlichkeiten für die angegebenen Zahlen als gekürzten Bruch ein.
 |
als gekürzter Bruch |
|||
| a) eine Zahl < 2 | ||||
| b) eine Zahl > 1 | ||||
| c) eine gerade Zahl | ||||
| d) eine Zahl > 2 | ||||
Versuche: 0
Aufgabe 27: Wie groß beim unteren Glücksrad ist die Wahrscheinlichkeit, auf Feld A oder C zu gelangen?

|
Versuche: 0
Aufgabe 28: Der batteriebetriebene Roboter bewegt sich in einer rein zufälligen Schrittfolge auf dem Buchstabenfeld hin und her. Mit welcher Wahrscheinlichkeit geht ihm die Batterie auf den folgenden Feldern aus und er bleibt stehen?
Antwort: Mit folgender Wahrscheinlichkeit bleibt er stehen auf:
| Feld A: | 1 | 
|
| Feld H: | 1 | |
| Feld I: | 1 | |
| Feld A, E oder I: | 1 | |
| Feld C oder G: | 1 | |
Versuche: 0
Aufgabe 29: Die 32 Karten eines Skat-Spieles liegen verdeckt auf dem Tisch. Mit welcher Wahrscheinlichkeit werden folgende Karten gezogen? Kürze die Brüche so weit wie möglich.

| a) Kreuz-Bube | b) ein Bild | c) kein Bild | |||
| d) ein König | e) ein Herz | f) keine Dame | |||
Versuche: 0
Aufgabe 30: Eine Lostrommel ist gefüllt mit 50% Nieten, 31% Trostpreise, 17% großen Preisen und 4 Hauptgewinnen.
a) Wie groß ist die Wahrscheinlichkeit einen Hauptgewinn zu ziehen? b) Wie viele Lose befinden sich in der Trommel? |
a) Die Wahrscheinlichkeit, einen Hauptgewinn zu ziehen, liegt bei %. b) Es befinden sich Lose in der Losttrommel. |
Versuche: 0
Aufgabe 31: In einer Lostrommel sind 32 Nieten und 8 Gewinne. Kreuze an, wie sich die Gewinnwahrscheinlichkeit jeweils verändert, wenn ...
| Gewinnwahrscheinlichkeit | |||
| wird größer |
bleibt gleich |
wird kleiner |
|
| a) ein Gewinn und eine Niete hinzugefügt werden. | |||
| b) ein Gewinn und 3 Nieten entfernt werden. | |||
| c) 3 Gewinne und 12 Nieten hinzugefügt werden. | |||
| d) 2 Gewinne und 8 Nieten entfernt werden. | |||
| e) 5 Gewinne und 19 Nieten hinzugefügt werden. | |||
Versuche: 0
Aufgabe 32: Wie hoch ist die Wahrscheinlichkeit, aus Losen einen der Hauptgewinne zu ziehen?
Die Wahrscheinlichkeit liegt bei %.
richtig: 0falsch: 0
Aufgabe 33: Bei der Feier einer Firma sollen alle 175 Angestellte ein Los ziehen können. Die Wahrscheinlichkeit, einen Gewinn zu ziehen, soll bei 20 % liegen. Die restlichen Lose sind Trostpreise. Wie viele Lose sind als Gewinn ausgezeichnet?
In der Lostrommel befinden sich Gewinne.
richtig: 0falsch: 0
Aufgabe 34: In einem Sack befinden sich 24 Kugeln in 3 unterschiedlichen Farben. Ein Drittel der Kugeln ist blau. Von den grünen Kugeln gibt es 4 weniger als von den roten. Wie groß ist die Wahrscheinlichkeit, eine grüne Kugel zu ziehen?
Die Wahrscheinlichkeit, eine grüne Kugel zu ziehen, liegt bei %.
richtig: 0falsch: 0
Aufgabe 35: Von den 20 Kugeln in einem Sack sind 40 % rot. 9 Kugeln sind weiß und die restlichen Kugeln sind blau. Wie wahrscheinlich ist es, eine blaue Kugel zu ziehen?
Die Wahrscheinlichkeit, eine blaue Kugel zu ziehen, liegt bei %.
Versuche: 0
Aufgabe 36: In zwei Schalen befinden sich jeweils drei Kugeln. In Schale (A) befindet sich eine grüne, eine rote und eine gelbe. Schale (B) ist mit einer blauen, einer roten und einer gelben Kugel befüllt. Ohne hinzusehen wird aus jeder Schale eine Kugel gezogen und auf den Tisch gelegt. Wie wahrscheinlich ist es, dass zwei verschiedenfarbige Kugeln auf dem Tisch liegen?

| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
Aufgabe 37: Berechne die Wahrscheinlichkeit, dass nach dem Drehen beider Zeiger mindestens einer auf einem Marienkäferfeld stehen bleibt.

| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
Aufgabe 38: Die unteren Buchstaben A, B und C erscheinen mit gleicher Wahrscheinlichkeit in allen möglichen Abfolgen. Wie wahrscheinlich ist es, dass die Buchstabenfolge B, C, A stehen bleibt? Gib die Lösung als gekürzten Bruch an.
| A | B | C |
| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
Aufgabe 39: Die unteren Buchstaben A, B, C und D erscheinen mit gleicher Wahrscheinlichkeit in allen möglichen Abfolgen. Wie wahrscheinlich ist es, dass die Buchstabenfolge B, D, A, C stehen bleibt? Gib die Lösung als gekürzten Bruch an.
| A | B | C | D |
| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
Aufgabe 40: Jenny und Felix würfeln. Jeder hat einen der abgebildeten Würfel.
| W | A | |||||||
| W | A | L | L | W | A | H | L | |
| L | L | |||||||
| Wie groß ist die Wahrscheinlichkeit, dass sie | |||||
| a) | gleichzeitig den gleichen Buchstaben würfeln? |
|
|||
| b) | verschiedene Buchstaben würfeln? |
|
|||
| c) | nur Vokale würfeln? |
|
|||
| Kürze deine Ergebnisse jeweils soweit wie möglich. | |||||
Versuche: 0