Kreis 
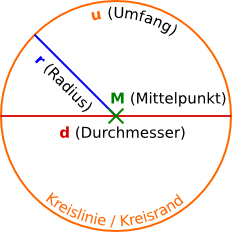
In einem Kreis haben alle Punkte des Umfangs den gleichen Abstand zum Mittelpunkt.
Hier kannst du ...
- Kreisgrößen kennenlernen (A 1 - A 2),
- Kreisumfänge und Kreisbögen bestimmen (A 3 - A 34),
- Kreisflächen bestimmen (A 35 - A 67).
Wichtige Kreisgrößen
Aufgabe 1: Klick jeweils den Begriff an, der in den roten Rahmen gehört.
|
d
Durchmesser
Mittelpunkt
r
Radius
Umfang
|
Aufgabe 2: Klick auf die Zahlen und trage die gesuchten Begriffe ein.
|
Kreisumfang
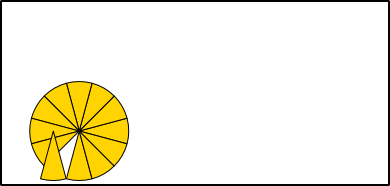
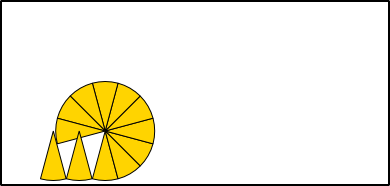
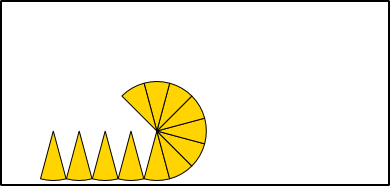
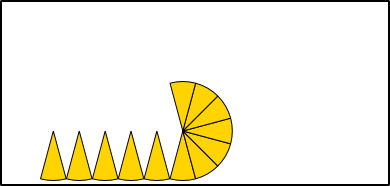
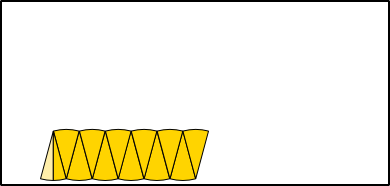
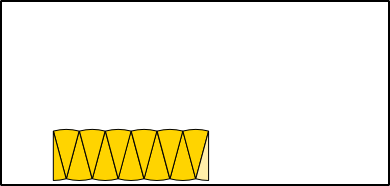
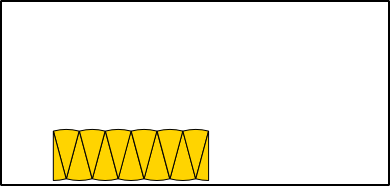
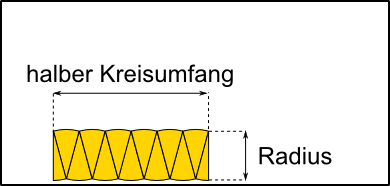
Ungefähre Umfangbestimmung
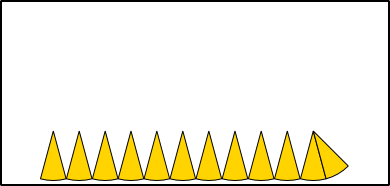
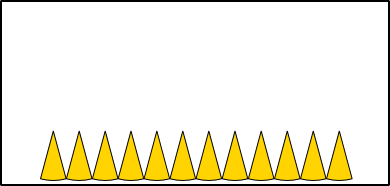
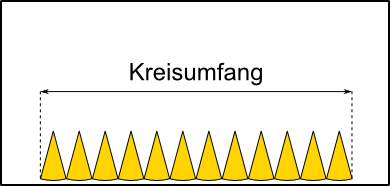
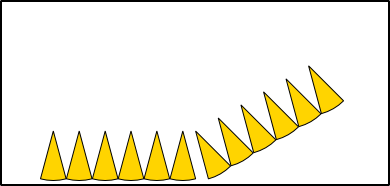
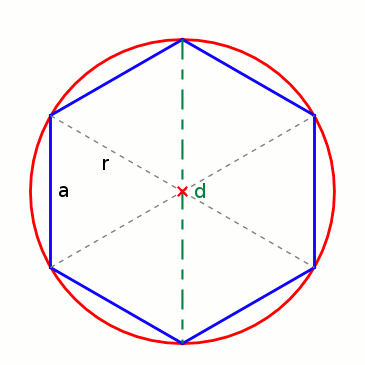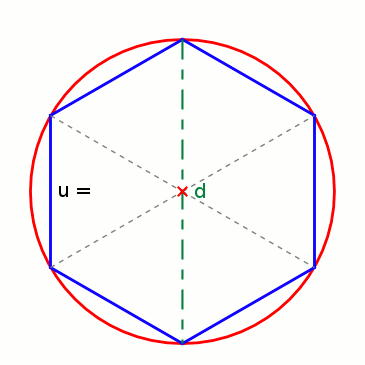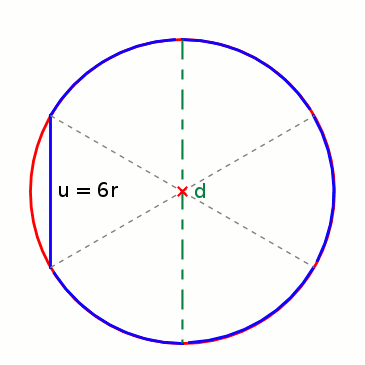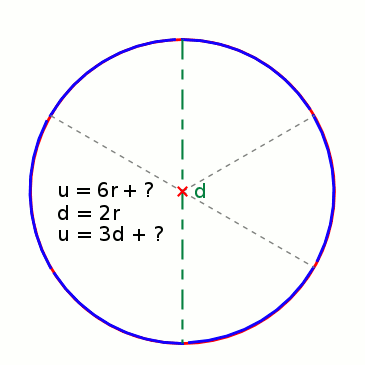
Aus 6 Radien (r) können die Seiten (a) eines Sechsecks gebildet werden, das genau in einen Kreis mit entsprechendem Radius hineinpasst. Werden die Seiten an den Kreisumfang angepasst, bleibt jeweils ein kleiner Rest, um den Umfang ganz schließen zu können. Der Umfang eines Kreises ist also so lang wie 3 Mal der Durchmesser (6 · r) plus einem Rest. Wie groß aber ist dieser Rest genau?
Kreiszahl Pi (π = 3,141592...)
Die Kreiszahl π gibt das Verhältnis zwischen dem dem Umfang (u) und Durchmesser (d) eines Kreises an. Für jeden Kreis gilt, dass sein Durchmesser genau π mal in seinen Umfang passt.
Aufgabe 3: Rolle mit dem orangen Gleiter unterschiedlich große Kreise ab und klicke anschließend unten die Daten die jeweils in das rote Kästchen gehören.
|
Merke:
Der Kreisdurchmesser passt genau , ...
Mal in den Kreisumfang hinein. Die Kreiszahl π ist , ... Umfangformel: = · π
1
1
3
3
4
4
d
u
|
Aufgabe 4:
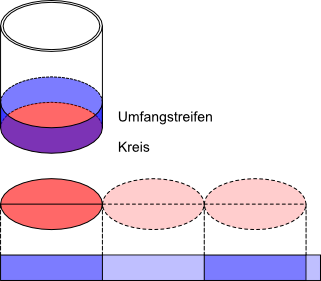
- Zeichne die Bodenfläche eines zylindrischen Glases (einen Kreis) auf ein Stück Pappe.
- Knick den Pappkreis hälftig (Durchmesser).
- Lege eine Pappstreifen um das Glas herum und schneide ihn auf Umfanglänge ab.
- Wie viele Durchmesser des Kreises kannst du auf den Umfangstreifen aneinanderreihen?
Formeln
Folgende Formeln spielen bei der Umfangberechnung eine wichtige Rolle:
| Umfang | u = d · π | |||||
| u = 2 · r · π | → | u = 2r · π | ||||
| Durchmesser | d = u : π | → |
|
|||
| Radius | r = u : π : 2 | → |
|
Aufgabe 5: Klick auf den Kreis, der den in der unteren Formel gesuchten Kreisteil symbolisiert (Umfang, Durchmesser, Radius). Bei richtigem Klick wird die Zahl Pi um die Ziffer als Nachkommastelle erweitert, die sich im entsprechenden Kreis bewegt. Du kannst hier auf 500 Nachkommastellen kommen.
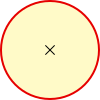
0 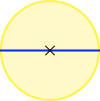
1

2
|
π = 3,14
richtig: 0 | falsch: 0
Aufgabe 6: Trage die richtigen Kreisumfänge ein. Runde das Ergebnis auf eine Nachkommastelle.
a) cm | b) cm | c) cm
richtig: 0falsch: 0
Aufgabe 7: Trage die richtigen Kreisumfänge ein. Das Ergebnis ist auf eine Nachkommastelle gerundet.
| d |
u |
|
d |
u |
|
d |
u |
| a) 1 cm |
,14 cm |
d) 10 cm |
,4 cm |
g) 100 cm |
,2 cm |
||
| b) 2 cm |
,28 cm |
e) 20 cm |
,8 cm |
h) 200 cm |
,3 cm |
||
| c) 3 cm |
,42 cm |
f) 30 cm |
,2 cm |
i) 300 cm |
,5 cm |
Versuche: 0
Aufgabe 8: Trage die richtigen Durchmesser ein. Runde auf ganze Zentimeter.
| u |
d |
|
u |
d |
|
u |
d |
| a) 25,1 cm |
cm |
d) 44 cm |
cm |
g) 84,8 cm |
cm |
||
| b) 15,7 cm |
cm |
e) 56,5 cm |
cm |
h) 100,5 cm |
cm |
||
| c) 28,3 cm |
cm |
f) 66 cm |
cm |
i) 125,6 cm |
cm |
Versuche: 0
Aufgabe 9: Trage die ganzen Zahlen der Kreisdaten ein. Die gerundete Nachkommastelle ist vorgegeben!
| r | d | u | |
| a) | cm | cm | ,0 cm |
| b) | cm | cm | ,2 cm |
| c) | cm | cm | cm |
richtig: 0falsch:
0
Aufgabe 10: Du siehst einen Ausschnitt aus dem Plan eines Fußballfeldes. Welchen Umfang hat der Anstoßkreis?
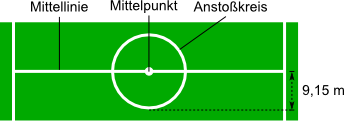
Der Anstoßkreis hat einen Umfang von ,5 m.
Versuche: 0
Aufgabe 11: Klick unten auf den "AUTO"-Button und schau dir an, wie man Umfänge von Teilkreisen berechnet.
© 2000 - http://geonext.de
 |
|||||
|
Aufgabe 12: Die Bogenlänge eines Teilkreises berechnet man, indem die Bogenlängen möglicher Kreisteile ermittelt werden. Trage in die unteren Textfelder die Bogenlänge der entsprechenden Teilkreise ein, wenn der Umfang des Vollkreises 16 cm beträgt.
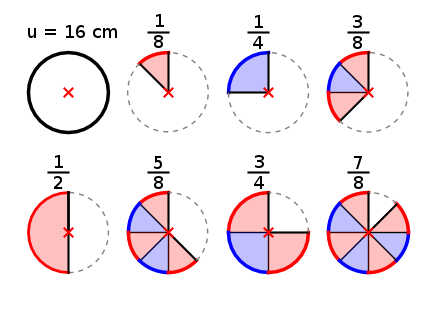
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
Versuche: 0
Aufgabe 13: Trage die richtigen Werte der orangen Kreisbögen ein. Die gerundete Nachkommastelle ist vorgegeben!
| Sektor | Bogenlänge | |
| a) | , cm | |
| b) | , cm | |
| c) | , cm | |
| d) | , cm | |
| e) | , cm | |
richtig: 0falsch: 0
Aufgabe 14: Trage die richtigen Werte der Umfänge der Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
| Figur | Umfang | |
| a) | , cm | |
| b) | , cm | |
| c) | , cm | |
| d) | , cm | |
| e) | , cm | |
richtig: 0falsch: 0
Aufgabe 15: Trage die Umfänge der Figuren ein.
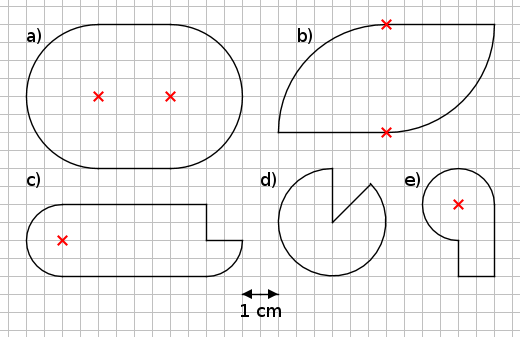
Die Figuren haben folgende Umfänge:
a) = ,6 cm | b) = ,4 cm | c) = ,7 cm
d) = ,2 cm | e = ,7 cm
Versuche: 0
Aufgabe 16: Trage den Umfang der folgenden Figur ein.
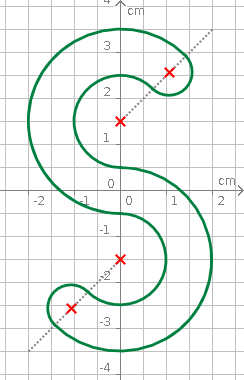
Das "S" hat einen Umfang von ,7 cm.
Versuche: 0
Aufgabe 17: Trage die richtigen Umfänge der grünen Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
| Figur | Umfang (u) |
| a) | , cm |
| b) | , cm |
| c) | , cm |
| d) | , cm |
richtig: 0falsch: 0
Aufgabe 18: Trage den Umfang der Figur unten ein. Runde auf eine Nachkommastelle.
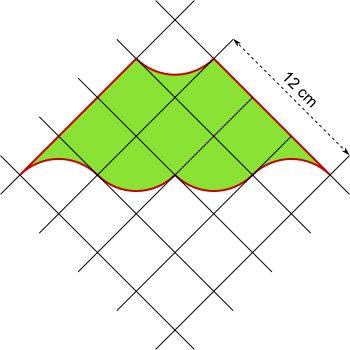
Der Umfang beträgt cm.
Versuche: 0
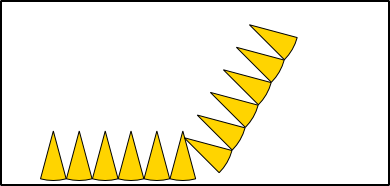
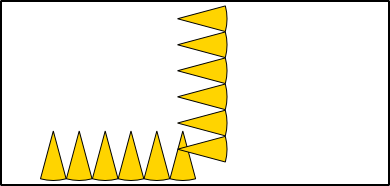
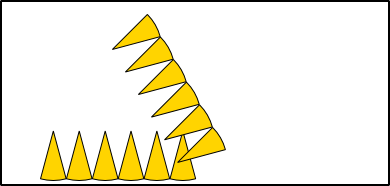
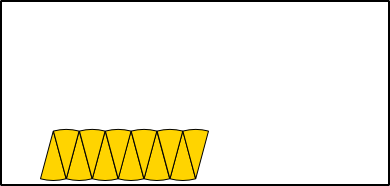
Aufgabe 19: Die folgende Spirale besteht aus 8 Viertelkreisen. Trage den Umfang der Spirale unten ein.
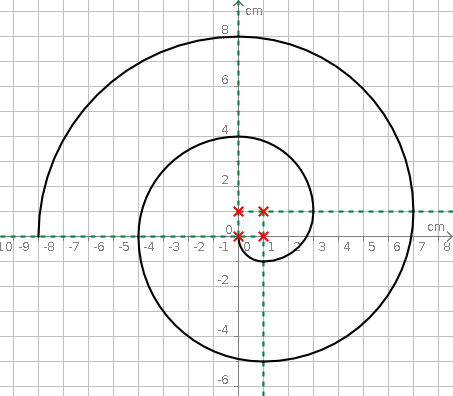
Die Spirale hat einen Umfang von ,5 cm.
Versuche: 0
Aufgabe 20: Trage den Umfang der Figur unten ein. Runde auf ganze Zentimeter.
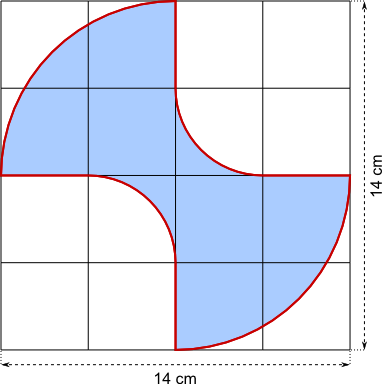
Der Umfang beträgt cm.
Versuche: 0
Aufgabe 21: Trage den Umfang der dargestellten "2" unten ein.
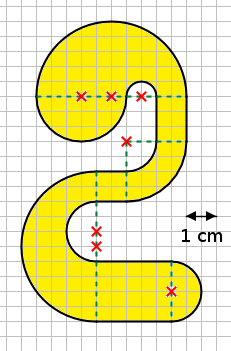
Die dargestellte "2" hat einen Umfang von ,0cm.
Versuche: 0
Aufgabe 22: Ziehe die beiden orangen Punkte der Grafik und beobachte die stattfindenden Veränderungen. Klick anschließend so auf die unteren Begriffe, dass der Satz richtig zusammengefügt wird.
|
Die Umfänge
genauso groß wie
sind zusammengenommen immer
des blauen und des
orangen Kreises.
grünen Kreises
der Umfang des
|
Versuche: 0
Aufgabe 23: Trage den ganzzahligen Umfang jeder Figur unten ein.
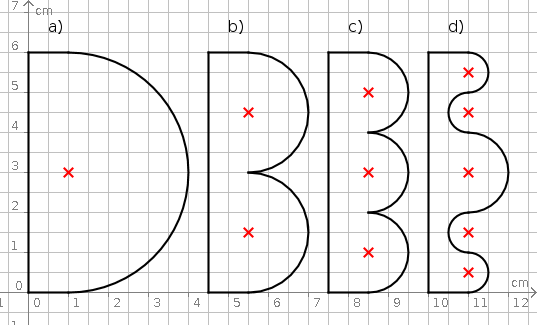
Die Figuren haben folgende Umfänge:
a) = ,4 cm | b) = ,4 cm | c) = ,4 cm | d) = ,4 cm
Versuche: 0
Aufgabe 24: Kreis a hat einen Umfang von 100 cm. Der Umfang von Kreis b ist 44 cm größer, also 144 cm. Kreis c hat ebenfalls einen 44 cm größeren Umfang (188 cm) als der vorhergehende Kreis. Trage ein, wie viel cm der Durchmesser der nachfolgenden Kreise jeweils größer ist. Runde auf ganze cm.
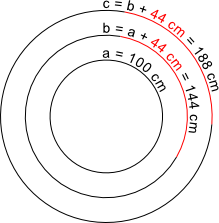
Der Durchmesser von Kreis b ist cm größer als der Durchmesser von Kreis a. Der Durchmesser von Kreis c ist cm größer als der Durchmesser von Kreis b. |
Versuche: 0
Aufgabe 25: Ein kreisrundes Steinkunstwerk mit einem Umfang von 10 m ist gleichmäßig von einer 44 cm längeren Kupferschiene (10,44 m) umrahmt. Wie groß ist der Abstand zwischen Stein und Schiene? Runde auf ganze cm.
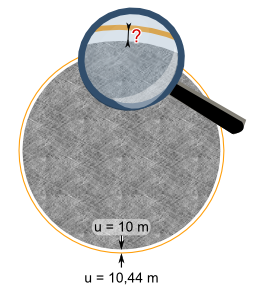
Die Schiene läuft in einem Abstand von cm um den Stein herum.
Versuche: 0
Aufgabe 26:Ein Schreiner soll aus zwei halbkreisförmigen Holzplatten einen Tisch erstellen, der an einem Balkonpfeiler zu befestigen ist. Der Pfeiler hat einen Umfang von cm. Welchen Radius hat das Loch des Tisches? Trage den ganzzahligen Radius unten ein.
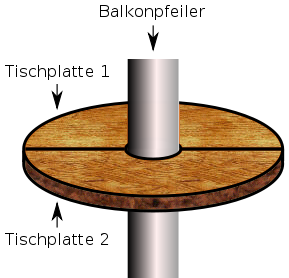
Das Loch hat einen Radius von cm.
Versuche: 0
Aufgabe 27: Die vordere Scheibe eines Riehmenantriebs hat einen Radius von 12 cm. Wie oft dreht sich die hintere Scheibe bei einem Radius von 6, 4 oder 3 cm um sich selbst, wenn die vordere Scheibe eine Umdrehung gemacht hat?
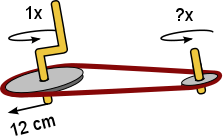
|
Radius
vorn |
Radius
hinten |
Umdrehungen
hinten |
| 12
cm |
6 cm | ||
| 4 cm | |||
| 3 cm |
Versuche: 0
Aufgabe 28: Die Größe von Fahrrädern wird in der bei uns veralteten Längeneinheit Zoll angegeben. 1 Zoll entspricht 2,54 cm. Trage unten ein, welchen Durchmesser und welchen Umfang die für die entsprechende Altersangabe empfohlenen Kinderräder haben.
| Kinderfahrrad Größenempfehlung | |||
| Alter bei normaler Körpergröße |
Radgröße in Zoll |
Durchmesser in cm |
Umfang in cm |
| 2 - 4 Jahre | 12 Zoll | ,48 | ,8 |
| 4 - 5 Jahre | 16 Zoll | ,64 | ,7 |
| 5 - 6 Jahre | 18 Zoll | ,72 | ,6 |
| 6 - 8 Jahre | 20 Zoll | ,80 | ,6 |
| 8 - 10 Jahre | 24 Zoll | ,96 | ,5 |
Versuche: 0
Aufgabe 29: Hochräder haben unterschiedliche Raddurchmesser. Welche Strecke legen Hochräder mit folgenden Raddurchmessern zurück, wenn sie 10 Umdrehungen gemacht haben? Trage die fehlenden Meter-Werte ein.

|
Raddurchmesser | zurückgelegte Strecke nach 10 Umdrehungen |
| 1,10 m | ,56 m | |
| 1,20 m | ,70 m | |
| 1,30 m | ,84 m | |
| 1,40 m | ,98 m | |
| 1,50 m | ,12 m | |
|
Fotothek df pk 0000316 027
Pfingsten 1947.jpg
von: Deutsche Fotothek Lizenz: CC BY-SA 3.0 Original: Hier |
||
Versuche: 0
Aufgabe 30: Martin fährt mit einem 20-Zoll-Einrad eine Strecke, für die er 42 Umdrehungen benötigt. Wie viel Umdrehungen benötigt Martina mit ihrem 24-Zoll-Einrad für dieselbe Strecke?
Martina benötigt Umdrehungen.
Versuche: 0
Aufgabe 31: Wie viele Umdrehungen benötigt Mathilda mit ihrem 20-Zoll-Einrad, um die 400 Meter einer Stadionrunde zurückzulegen? Ein Zoll entspricht 2,54 cm. Trage den fehlenden ganzzahligen Wert ein.
Sie schafft die Strecke mit ,6 Umdrehungen.
Versuche: 0
|
Aufgabe 32: Die Turmuhr des Elizabeth Towers (Big Ben) hat ein Zifferblatt mit einem Durchmesser von 7 m. Welche Strecke legt die Spitze des Minutenzeigers, die sich genau entlang des Zifferblattrandes bewegt, in einer Stunde, an einem Tag und in einem Jahr zurück? Runde auf ganze Meter (Kilometer).
Versuche: 0 |
|
Aufgabe 33: In einer verbesserten Version des Patent-Motorwagen Nummer 1 absolvierte Bertha Benz 1888 die erste Fernfahrt der Automobilgeschichte. Sie fuhr über Umwege von Mannheim nach Pforzheim und zurück. Dabei überwand sie eine Strecke von 180 km. Das Vorderrad hatte einen Durchmesser von 730 mm, der Durchmesser der Hinterräder betrug je 1125 mm. Wie viele Umdrehungen machte auf dieser Strecke das Vorderrad und wie oft drehten sich die Hinterräder um sich selbst? Runde auf 1000er.

|
|
Versuche: 0
Aufgabe 34: Krümel schafft in 7 Sekunden 12 Runden in seinem Hamsterrad. Das Rad hat einen inneren Durchmesser von 25 cm. Mit welcher Geschwindigkeit (km/h) bewegt sich Krümel im Schnitt? Runde auf eine Nachkommastelle.
Krümel bewegt sich mit einer Geschwindigkeit von km/h.
Versuche: 0
Aufgabe 35: Windräder vom Typ E-126 haben einen Rotordurchmesser von 127 m und eine variable Drehzahl von 5 - 11,7 Umdrehungen pro Minute. Mit wie viel km/h bewegen sich die äußeren Rotorspitzen bei minimaler und bei maximaler Drehzahl? Runde auf ganze km/h.

Die Rotorspitzen haben bei 5 U/min ein Tempo von km/h. Bei 11,7 U/min bewegen sie sich mit einer Geschwindigkeit von km/h.
Versuche: 0
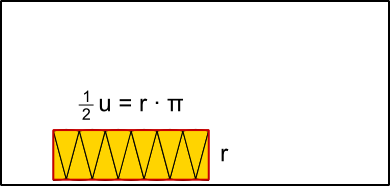
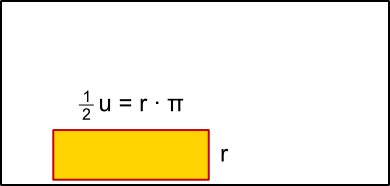
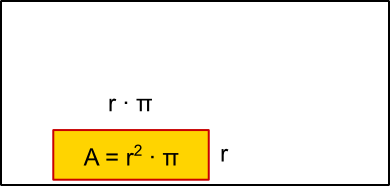
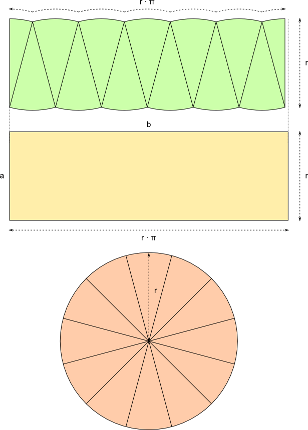
Aufgabe 36: Klick auf die "Auto"-Schaltfläche. Betrachte die Animation genau und klick die richtigen Begriffe des Erklärungstextes an.

Flächenformel: = · π
Versuche: 0
Aufgabe 37: Lege die Aufgabe 36 auf Papier nach. Dafür kannst du die entsprechende Grafik einer PDF-Datei ausdrucken, die bei einem Klick auf das Bild erscheint.
Aufgabe 38: Trage die richtigen Flächeninhalte der Kreise ein. Runde das Ergebnis auf eine Nachkommastelle.
|
a) cm2 | b) cm2 | c) cm2
|
Aufgabe 39: Trage die richtigen Flächeninhalte ein. Das Ergebnis ist auf eine Nachkommastelle gerundet.
| r |
A |
|
r |
A |
|
r |
A |
| a) 1 cm |
,1 cm² |
d) 4 cm |
,3 cm² |
g) 7 cm |
,9 cm² |
||
| b) 2 cm |
,6 cm² |
e) 5 cm |
,5 cm² |
h) 8 cm |
,1 cm² |
||
| c) 3 cm |
,3 cm |
f) 6 cm |
,1 cm |
i) 9 cm |
,5 cm |
Versuche: 0
Aufgabe 40: Trage die richtigen Flächeninhalte der Ringe ein. Runde das Ergebnis auf eine Nachkommastelle.
![]()
|
a) cm2 | b) cm2 | c) cm2 richtig: 0falsch: 0 |
Aufgabe 41: Den Flächeninhalt (A) eines Teilkreises berechnet man, indem die Flächeninhalte möglicher Kreisteile ermittelt werden. Trage in die unteren Textfelder die Flächeninhalte der entsprechenden Teilkreise ein, wenn der Flächeninhalt des Vollkreises 24 cm2 beträgt.
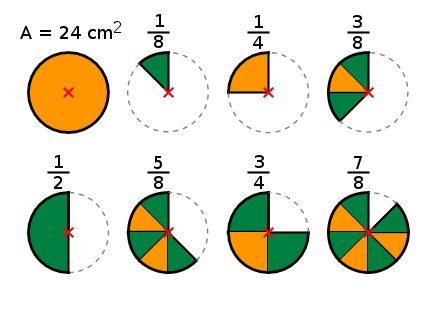
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
Versuche: 0
Aufgabe 42: Trage die richtigen Werte der orangen Kreisbögen und der farbigen Kreisflächen ein. Die gerundete Nachkommastelle ist vorgegeben!
| Sektor | a) Bogenlänge | b) Flächeninhalt |
| a) | , cm | , cm² |
| b) | , cm | , cm² |
| c) | , cm | , cm² |
| d) | , cm | , cm² |
| e) | , cm | , cm² |
|
|
|
Aufgabe 43: Ziehe die beiden Gleiter der Grafik und beobachte wie der Winkel des Kreissektors die Bogenlänge und den Flächeninhalt verändert.
| Vollkreis | Teilkreis | |||||
| r = 1 | d = 1 | ||||||
| Winkelanteil |
|
|
||||
| Bruchteil |
|
|
||||
| Bogenlänge | 1 |
|
||||
| Fläche | 1 |
|
||||
| gerundete Werte | ||||||
Aufgabe 44: Statt zu 8-teln kann man einen Kreis auch 360-steln, in Gradanteile zergliedern. Klick unten jeweils den erweiterten Bruch an, der in den roten Rahmen gehört.
|
|
|
|
|
|
|
|
||||||||||||||||
| 45 |
| 360 |
| 90 |
| 360 |
| 180 |
| 360 |
| 270 |
| 360 |
| 360 |
| 360 |
| 135 |
| 360 |
| 225 |
| 360 |
| 315 |
| 360 |
Versuche: 0
Aufgabe 45: Klick in der unteren Tabelle die richtigen Bogenlängen und Flächen an.
| Bogenlänge = Kreisumfang · | Mittelpunktswinkel |
| 360 |
| Sektorfläche = Kreisfläche · | Mittelpunktswinkel |
| 360 |
| a) | b) | c) | d) | e) | |
| Radius | |||||
| Mittlepunktswinkel | |||||
| Bogenlänge | |||||
| Fläche |
richtig: 0falsch: 0
Aufgabe 46: Trage die ganzen Zahlen der Kreisdaten ein. Die gerundete Nachkommastelle ist vorgegeben!
| r | d | uK | AK | |
| a) | cm | cm | ,0 cm | ,1 cm² |
| b) | cm | cm | ,2 cm | ,3 cm² |
| c) | cm | cm | cm | ,4 cm² |
richtig: 0falsch:
0
Aufgabe 47: Ein sich drehender Impuls-Rasensprenger hat eine Reichweite von 12 m. Trage die Fläche ein, die er bewässert.

Der Rasensprenger bewässert eine Fläche von ,4 m2 gesehen.
Versuche: 0
Aufgabe 48: Die "Elbe 1" war ein Feuerschiff, dass vor der Elbmündung lag um einfahrenden Schiffen aus der Nordsee die Richtung zu weisen. Sein Leuchtfeuer lag 15 Meter über der Wasserlinie und war 23 Seemeilen (Eine Seemeile = 1852 Meter) weit zu sehen. Auf wie viel Quadratkilometern Fläche konnte das Licht dieses Feuerschiffs gesichtet werden?

Das Licht dieses Schiffes wurde auf ,2 km2 gesehen.
Versuche: 0
Aufgabe 49: Ein quadratischer Holzstab hat eine Querschnittsfläche von 16 cm2. Aus ihm soll ein runder Holzstab gedrechselt werden. Trage unten die größtmögliche Querschnittsfläche dieses Rundholzes ein.
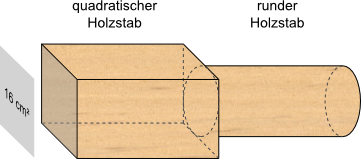
Der größtmögliche Querschnittsfläche des runden Stabes beträgt ,6 cm2
Versuche: 0
Aufgabe 50: Trage die richtigen Umfänge und Flächeninhalte der grünen Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
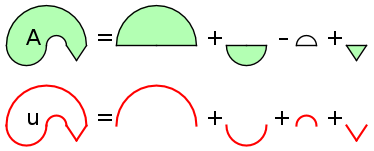
| Figur | a) Umfang (u) | b) Fläche (A) |
| a) | , cm | , cm² |
| b) | , cm | , cm² |
| c) | , cm | , cm² |
| d) | , cm | , cm² |
|
|
|
Aufgabe 51: Trage die Flächeninhalte der Figuren ein.
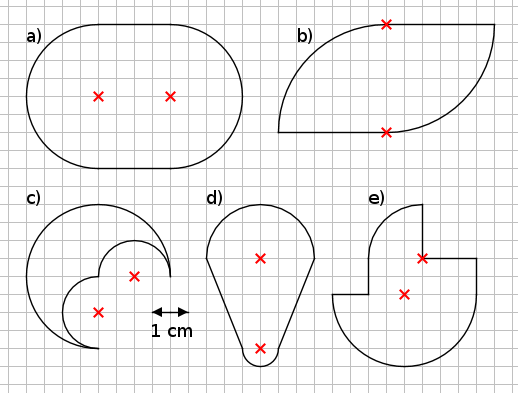 |
| Antwort: Die Figuren haben folgende Flächeninhalte:
a) = ,6 cm² | b) = ,1 cm² | c) = ,3 cm² d) = ,9 cm² | e = ,1 cm² |
Versuche: 0
Aufgabe 52: Trage den ganzzahligen Umfang (u) und Flächeninhalt (A) des großen Kreises und der beiden kleinen Kreise unten ein? Was fällt auf?
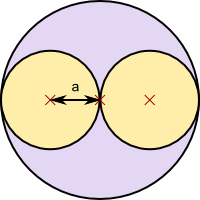
| a |
großer Kreis |
2 kleine Kreise |
| 1 cm |
u = ,6 cm A = ,56 cm² |
u = ,6 cm A = ,28 cm² |
| 2 cm |
u = ,1 cm A = ,26 cm² |
u = ,1 cm A = ,13 cm² |
| 3 cm |
u = ,7 cm A = ,10 cm² |
u = ,7 cm A = ,55 cm² |
Versuche: 0
Aufgabe 53: Nachdem du die obere Aufgabe gelöst hast, gib bitte unten die richtigen Zahlen an.
- Verdoppelt man den Radius eines Kreises, dann ist sein Flächeninhalt 22 Mal, also Mal so groß.
- Verdreifacht man den Radius eines Kreises, dann ist sein Flächeninhalt Mal, also Mal so groß.
- Vervierfacht man den Radius eines Kreises, dann ist sein Flächeninhalt Mal, also Mal so groß.
Versuche: 0
Aufgabe 54: Trage den Flächeninhalt (A) der gleichfarbigen Kreisbereiche unten ein.
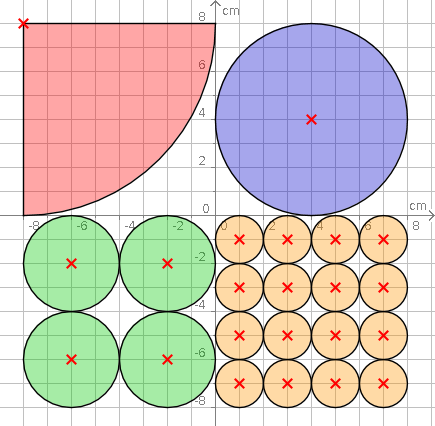 |
||
| ¼ Kreis | 1 Kreis | |
| r = 8 cm A = ,3 cm² |
r = 4 cm A = ,3 cm² |
|
| 4 Kreise | 16 Kreise | |
| r = je 2 cm A = ,3 cm² |
r = je 1cm A = ,3 cm² |
|
Versuche: 0
Aufgabe 55: Trage den Flächeninhalt des grünen Bereichs der folgenden Figur unten ein.
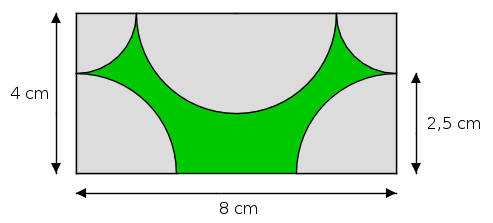
Der Flächeninhalt beträgt ,8 cm².
Versuche: 0
Aufgabe 56: Trage den Flächeninhalt der folgenden Figur unten ein.
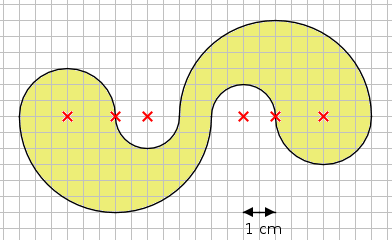
Der Flächeninhalt beträgt ,2 cm².
Versuche: 0
Aufgabe 57: Trage den Flächeninhalt der folgenden Figur unten ein.
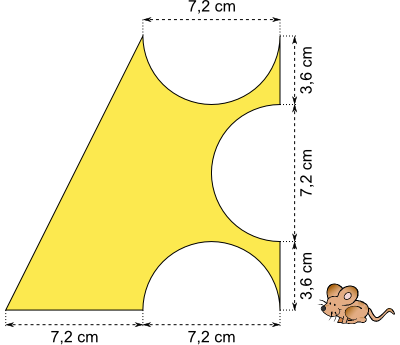
Der Flächeninhalt beträgt ,4 cm2
Versuche: 0
Aufgabe 58: Trage den Flächeninhalt der folgenden Figur unten ein.
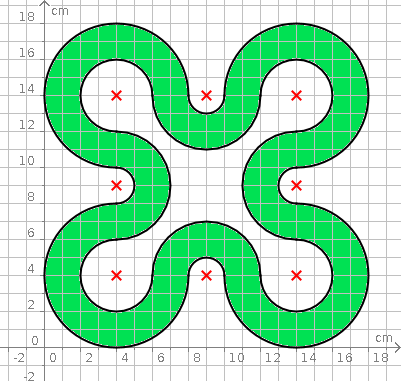
Der Flächeninhalt beträgt ,4 cm².
Versuche: 0
Aufgabe 59: Trage den Flächeninhalt der schräg liegenden Acht unten ein.
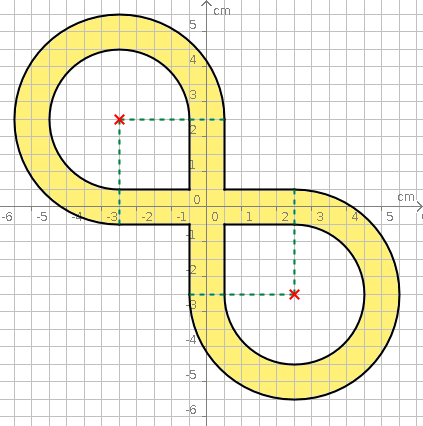
Der Flächeninhalt beträgt ,6 cm².
Versuche: 0
Aufgabe 60: Ein Künstler bemalt eine Hauswand mit folgendem Motiv. Er benötigt 1,5 Liter Farbe je Quadratmeter. Wie viel Farbe verbraucht er für das Bild?

Der Flächeninhalt beträgt ,9 cm².
Versuche: 0
Aufgabe 61: Der grüne Ring hat eine Fläche von und einen Durchmesser von . Wie groß ist der Radius des Ringloches? Runde auf eine Nachkommastelle.
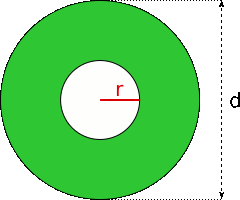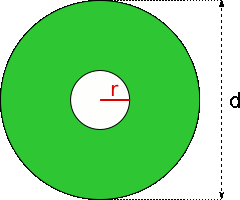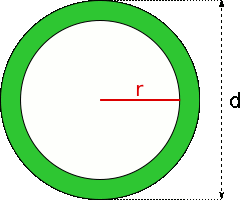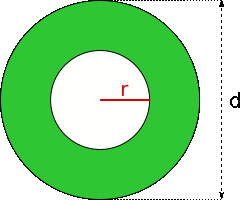
Der Radius des Loches beträgt cm.
richtig: 0falsch: 0
Aufgabe 62: Trage die Fläche des gelben Quadrates und die Summe der grünen Flächen unten ein.
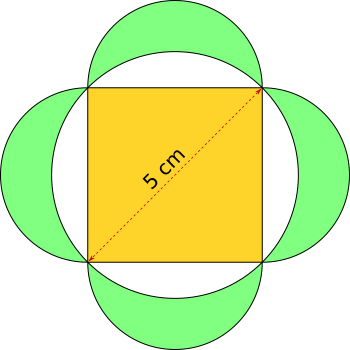
A gelbes Quadrat = cm² | A grüne Flächen = cm²
Versuche: 0
Aufgabe 63: Ein kreisförmiges Beet hat einen Durchmesser von 11 m. Der Gärtner rechnet mit 8 Pflanzen pro m². Wie viele Pflanzen benötigt er?
Der Gärtner benötigt Pflanzen.
Versuche: 0
Aufgabe 64:
- Für eine kreisförmige Tischplatte mit 1,20 m Durchmesser soll eine Tischdecke genäht werden. Die Decke soll etwa 20 cm überhängen. Aus wie viel m² Stoff besteht die Decke?
- Um die Decke herum soll eine Bordüre befestigt werden. Wie viel Meter Bordüre werden benötigt?
|
Runde auf Einer.
Versuche: 0 |
Aufgabe 65: Um einen runden Teich mit 24 m Durchmesser verläuft nach einem Uferstreifen von 30 cm ein Weg mit einer Breite von 1,50 m. Wie viel m² nimmt die Wegfläche ein? Runde auf ganze m² auf.
Der Weg hat eine Fläche von m².
Versuche: 0
Aufgabe 66: Der Umfang eines Kreises hat die gleiche Länge wie der Umfang eines Quadrates mit einer Seitenlänge von a = . Welche Flächeninhalt hat der Kreis? Trage den fehlenden ganzzahligen Wert ein.
Der Kreis hat einen Flächeninhalt von , cm²
richtig: 0falsch: 0
Aufgabe 67: Windräder vom Typ E-126 haben einen Rotordurchmesser von 127 m. Auf dem Bild unten sieht man 11 Windräder vom Typ E-126. Ein normales Fußballfeld ist 68 m breit und 105 m lang. Den Platz von wie vielen Fußballfeldern nimmt die Rotationsfläche der dargestellten Windräder ein? Runde auf ganze Fußballfelder auf.

Die Rotationsfläche der 11 Windräder nimmt den Platz von etwa Fußballfeldern ein.
Versuche: 0
|
Aufgabe 68: Eine Bühne im Stadtpark soll die rechts angezeigte Form einnehmen. Welchen Umfang und welchen Flächeninhalt hat diese Bühne? Die Bühne hat einen Umfang von ,71 m und einen Flächeninhalt von ,56m². Versuche: 0 |
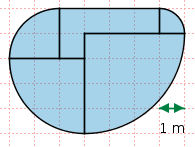
|