Kreisfläche
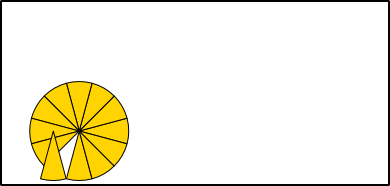
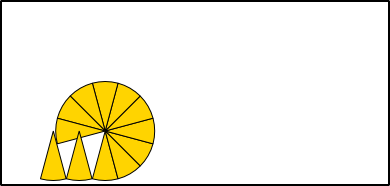
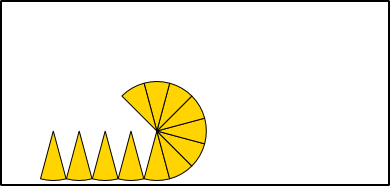
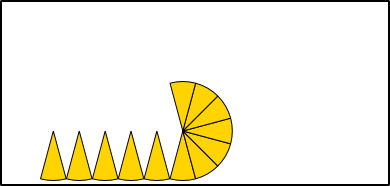
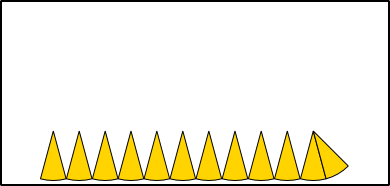
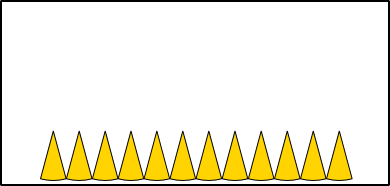
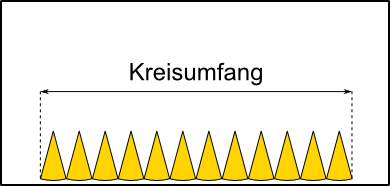
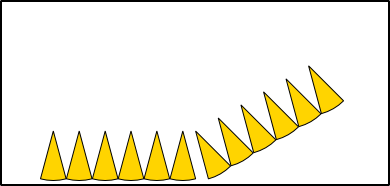
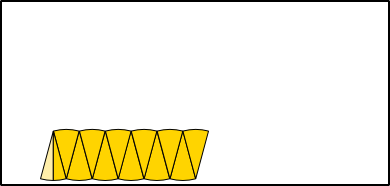
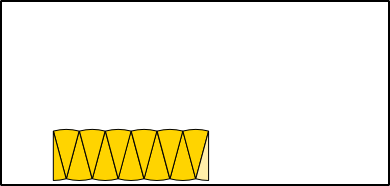
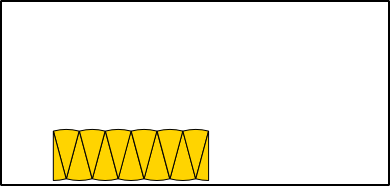
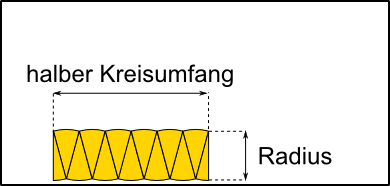
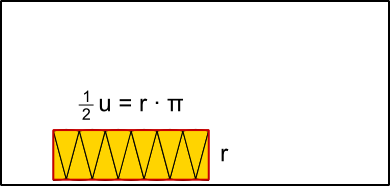
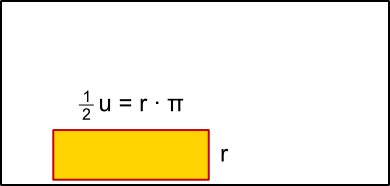
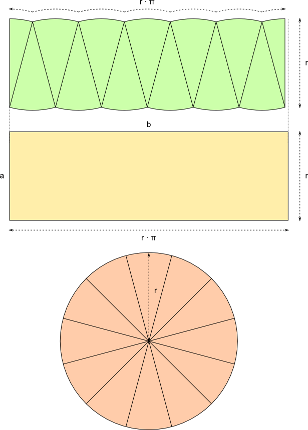
Aufgabe 1: Klick auf die "Auto"-Schaltfläche. Betrachte die Animation genau und klick die richtigen Begriffe des Erklärungstextes an.

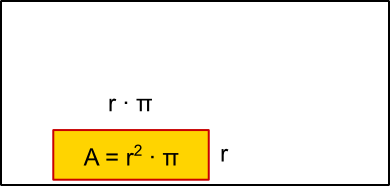
Flächenformel: = · π
Versuche: 0
Aufgabe 2: Lege die Aufgabe 1 auf Papier nach. Dafür kannst du die entsprechende Grafik einer PDF-Datei ausdrucken, die bei einem Klick auf das Bild erscheint.
Aufgabe 3: Trage die richtigen Flächeninhalte der Kreise ein. Runde das Ergebnis auf eine Nachkommastelle.
|
a) cm2 | b) cm2 | c) cm2
|
Aufgabe 4: Trage die richtigen Flächeninhalte ein. Das Ergebnis ist auf eine Nachkommastelle gerundet.
| r |
A |
|
r |
A |
|
r |
A |
| a) 1 cm |
,1 cm² |
d) 4 cm |
,3 cm² |
g) 7 cm |
,9 cm² |
||
| b) 2 cm |
,6 cm² |
e) 5 cm |
,5 cm² |
h) 8 cm |
,1 cm² |
||
| c) 3 cm |
,3 cm |
f) 6 cm |
,1 cm |
i) 9 cm |
,5 cm |
Versuche: 0
Aufgabe 5: Trage die richtigen Flächeninhalte der Ringe ein. Runde das Ergebnis auf eine Nachkommastelle.
![]()
|
a) cm2 | b) cm2 | c) cm2 richtig: 0falsch: 0 |
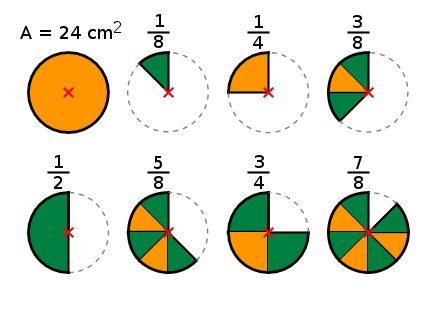
Aufgabe 6: Den Flächeninhalt (A) eines Teilkreises berechnet man, indem die Flächeninhalte möglicher Kreisteile ermittelt werden. Trage in die unteren Textfelder die Flächeninhalte der entsprechenden Teilkreise ein, wenn der Flächeninhalt des Vollkreises 24 cm2 beträgt.
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
Versuche: 0
Aufgabe 7: Trage die richtigen Werte der orangen Kreisbögen und der farbigen Kreisflächen ein. Die gerundete Nachkommastelle ist vorgegeben!
| Sektor | a) Bogenlänge | b) Flächeninhalt |
| a) | , cm | , cm² |
| b) | , cm | , cm² |
| c) | , cm | , cm² |
| d) | , cm | , cm² |
| e) | , cm | , cm² |
|
|
|
Aufgabe 8: Trage die ganzen Zahlen der Kreisdaten ein. Die gerundete Nachkommastelle ist vorgegeben!
| r | d | uK | AK | |
| a) | cm | cm | ,0 cm | ,1 cm² |
| b) | cm | cm | ,2 cm | ,3 cm² |
| c) | cm | cm | cm | ,4 cm² |
richtig: 0falsch:
0
Aufgabe 9: Ein sich drehender Impuls-Rasensprenger hat eine Reichweite von 12 m. Trage die Fläche ein, die er bewässert.

Der Rasensprenger bewässert eine Fläche von ,4 m2 gesehen.
Versuche: 0
Aufgabe 10: Die "Elbe 1" war ein Feuerschiff, dass vor der Elbmündung lag um einfahrenden Schiffen aus der Nordsee die Richtung zu weisen. Sein Leuchtfeuer lag 15 Meter über der Wasserlinie und war 23 Seemeilen (Eine Seemeile = 1852 Meter) weit zu sehen. Auf wie viel Quadratkilometern Fläche konnte das Licht dieses Feuerschiffs gesichtet werden?

Das Licht dieses Schiffes wurde auf ,2 km2 gesehen.
Versuche: 0
Aufgabe 11: Ein quadratischer Holzstab hat eine Querschnittsfläche von 16 cm2. Aus ihm soll ein runder Holzstab gedrechselt werden. Trage unten die größtmögliche Querschnittsfläche dieses Rundholzes ein.
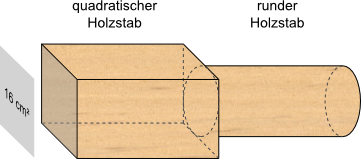
Der größtmögliche Querschnittsfläche des runden Stabes beträgt ,6 cm2
Versuche: 0
Aufgabe 12: Trage die richtigen Umfänge und Flächeninhalte der grünen Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
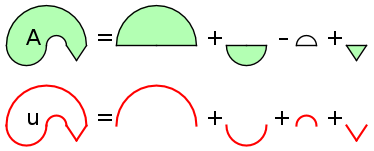
| Figur | a) Umfang (u) | b) Fläche (A) |
| a) | , cm | , cm² |
| b) | , cm | , cm² |
| c) | , cm | , cm² |
| d) | , cm | , cm² |
|
|
|
Aufgabe 13: Trage die Flächeninhalte der Figuren ein.
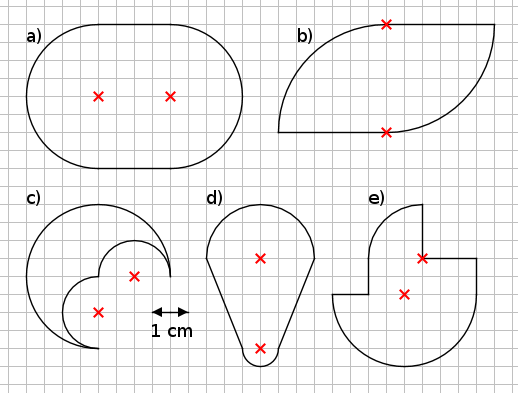 |
| Antwort: Die Figuren haben folgende Flächeninhalte:
a) = ,6 cm² | b) = ,1 cm² | c) = ,3 cm² d) = ,9 cm² | e = ,1 cm² |
Versuche: 0
Aufgabe 14: Trage den ganzzahligen Umfang (u) und Flächeninhalt (A) des großen Kreises und der beiden kleinen Kreise unten ein? Was fällt auf?
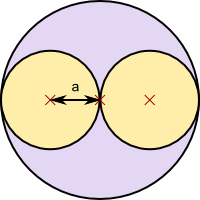
| a |
großer Kreis |
2 kleine Kreise |
| 1 cm |
u = ,6 cm A = ,56 cm² |
u = ,6 cm A = ,28 cm² |
| 2 cm |
u = ,1 cm A = ,26 cm² |
u = ,1 cm A = ,13 cm² |
| 3 cm |
u = ,7 cm A = ,10 cm² |
u = ,7 cm A = ,55 cm² |
Versuche: 0
Aufgabe 15: Nachdem du die obere Aufgabe gelöst hast, gib bitte unten die richtigen Zahlen an.
- Verdoppelt man den Radius eines Kreises, dann ist sein Flächeninhalt 22 Mal, also Mal so groß.
- Verdreifacht man den Radius eines Kreises, dann ist sein Flächeninhalt Mal, also Mal so groß.
- Vervierfacht man den Radius eines Kreises, dann ist sein Flächeninhalt Mal, also Mal so groß.
Versuche: 0
Aufgabe 16: Trage den Flächeninhalt (A) der gleichfarbigen Kreisbereiche unten ein.
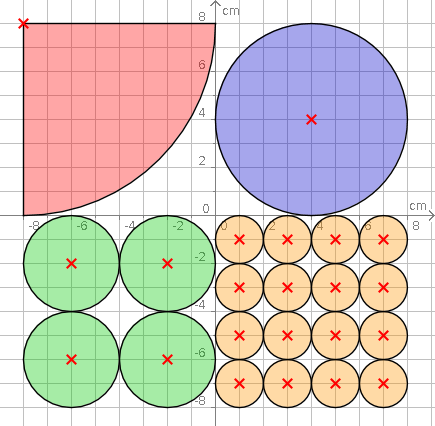 |
||
| ¼ Kreis | 1 Kreis | |
| r = 8 cm A = ,3 cm² |
r = 4 cm A = ,3 cm² |
|
| 4 Kreise | 16 Kreise | |
| r = je 2 cm A = ,3 cm² |
r = je 1cm A = ,3 cm² |
|
Versuche: 0
Aufgabe 17: Trage den Flächeninhalt des grünen Bereichs der folgenden Figur unten ein.
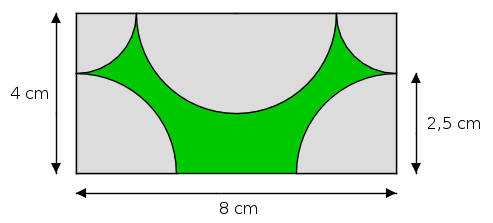
Der Flächeninhalt beträgt ,8 cm².
Versuche: 0
Aufgabe 18: Trage den Flächeninhalt der folgenden Figur unten ein.
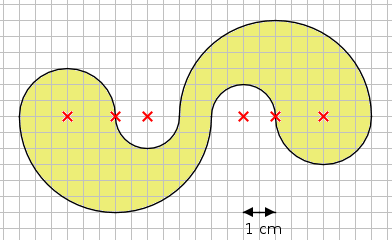
Der Flächeninhalt beträgt ,2 cm².
Versuche: 0
Aufgabe 19: Trage den Flächeninhalt der folgenden Figur unten ein.
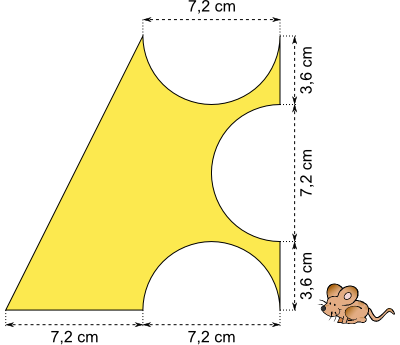
Der Flächeninhalt beträgt ,4 cm2
Versuche: 0
Aufgabe 20: Trage den Flächeninhalt der folgenden Figur unten ein.
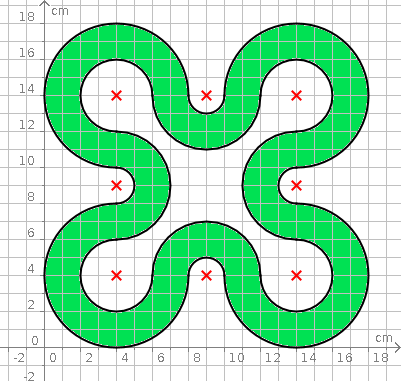
Der Flächeninhalt beträgt ,4 cm².
Versuche: 0
Aufgabe 21: Trage den Flächeninhalt der schräg liegenden Acht unten ein.
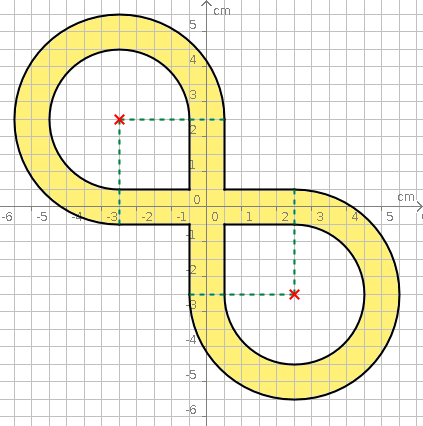
Der Flächeninhalt beträgt ,6 cm².
Versuche: 0
Aufgabe 22: Ein Künstler bemalt eine Hauswand mit folgendem Motiv. Er benötigt 1,5 Liter Farbe je Quadratmeter. Wie viel Farbe verbraucht er für das Bild?

Der Flächeninhalt beträgt ,9 cm².
Versuche: 0
Aufgabe 23: Der grüne Ring hat eine Fläche von und einen Durchmesser von . Wie groß ist der Radius des Ringloches? Runde auf eine Nachkommastelle.
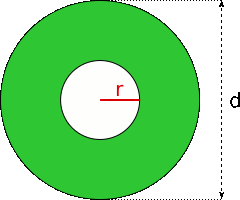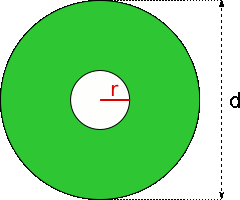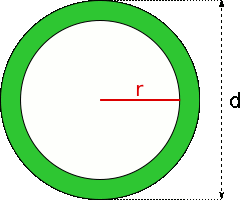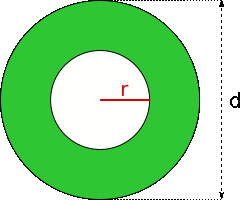
Der Radius des Loches beträgt cm.
richtig: 0falsch: 0
Aufgabe 24: Trage die Fläche des gelben Quadrates und die Summe der grünen Flächen unten ein.
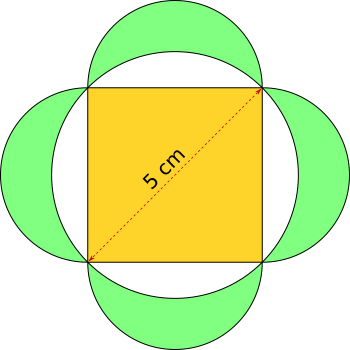
A gelbes Quadrat = cm² | A grüne Flächen = cm²
Versuche: 0
Aufgabe 25: Ein kreisförmiges Beet hat einen Durchmesser von 11 m. Der Gärtner rechnet mit 8 Pflanzen pro m². Wie viele Pflanzen benötigt er?
Der Gärtner benötigt Pflanzen.
Versuche: 0
Aufgabe 26:
- Für eine kreisförmige Tischplatte mit 1,20 m Durchmesser soll eine Tischdecke genäht werden. Die Decke soll etwa 20 cm überhängen. Aus wie viel m² Stoff besteht die Decke?
- Um die Decke herum soll eine Bordüre befestigt werden. Wie viel Meter Bordüre werden benötigt?
|
Runde auf Einer.
Versuche: 0 |
Aufgabe 27: Um einen runden Teich mit 24 m Durchmesser verläuft nach einem Uferstreifen von 30 cm ein Weg mit einer Breite von 1,50 m. Wie viel m² nimmt die Wegfläche ein? Runde auf ganze m² auf.
Der Weg hat eine Fläche von m².
Versuche: 0

Die Rotationsfläche der 11 Windräder nimmt den Platz von etwa Fußballfeldern ein.
Versuche: 0
|
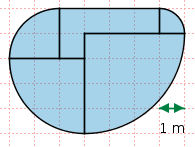
Aufgabe 29: Eine Bühne im Stadtpark soll die rechts angezeigte Form einnehmen. Welchen Umfang und welchen Flächeninhalt hat diese Bühne? Die Bühne hat einen Umfang von ,71 m und einen Flächeninhalt von ,56m². Versuche: 0 |
|