Test: Flächen

Aufgabe2: Trage die Vorkommastellen deiner auf zwei Nachkommastellen gerundeten Lösungen in den Test ein.

• Ergebnis: 141,371 → Eintrag: 141
• Ergebnis: 141,999 → Eintrag: 142

Hilfe
a)	r = d : 2	r = d : 2
b)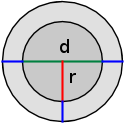
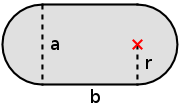c)	u : 2 = ?	u : 4 + 2 · r = ?
d)	AP = a · ha	AT = (a + c) : 2 · hc
e)	A½K = π · r² : 2 AR = a · b	AD = g · hg : 2 AT = (a + c) : 2 · hc A¼K = π · r² : 4

Neu
	Spaltenwertung Versuch 1: 2 Punkte Versuch 2: 1 Punkt	Spaltenwertung Versuch 1: 4 Punkte Versuch 2: 2 Punkte	P u n k t e
	Nur die beste Bewertung einer Zeile wird in die Gesamtbewertung übernommen.
a)	Trage den Umfang eines Kreises mit einem Radius von m ein. Antwort: Der Kreis hat einen Umfang von  m.	Trage den Radius eines Kreises mit einem Umfang von m ein. Antwort: Der Kreis hat einen Radius von  m.	0
b)	Ein rundes Loch hat einen Durchmesser von  m. Es soll mit einer kreisrunden Sperrholzplatte abgedeckt werden, die ringsum 6,4 cm übersteht. Aus wie viel m² Sperrholz besteht diese Platte. Antwort: Die Sperrholzplatte hat eine Deckfläche von m2.	Eine Verkehrsinsel besteht aus einem Rechteck, an dessen kürzeren Seiten je ein Halbkreis ansetzt. Das Rechteck ist m lang und m Breit. Welche Fläche nimmt die Verkehrsinsel ein? Antwort: Die Verkehrsinsel hat eine Fläche von m2.	0
c)	Trage die Länge des Kreisbogens ein. 7 dm Antwort: Der Kreisbogen hat eine Länge von  dm.	Trage den Umfang der Figur ein. dm Antwort: Die Figur hat einen Umfang von  dm.	0
Name		Klasse | Datum
d)	Berechne den Flächeninhalt der Figur. Antwort: Die Figur hat einen Flächeninhalt von  cm2	Berechne den Flächeninhalt der Figur. Antwort: Die Figur hat einen Flächeninhalt von  cm2	0
e)	Berechne den Flächeninhalt der zusammengesetzten Fläche. Antwort: Die Figur hat einen Flächeninhalt von  cm2	Berechne den Flächeninhalt der zusammengesetzten Fläche. Antwort: Die Figur hat einen Flächeninhalt von  cm2	0
	gesamt:           Versuche: 2 Auswertung		0