Parallelogramm
Ein Parallelogramm (Rhomboid) ist ein Viereck, bei dem die gegenüberliegende Seiten gleich lang und parallel sind.- Der Umfang des Parallelogramms ergibt sich aus der Summe der
vier Seitenlängen.
u = 2a + 2b - Ein Parallelogramm hat den Flächeninhalt eines Rechtecks mit
gleicher Seitenlänge und Höhe. Man berechnet ihn, indem die
Länge einer Seite mit der dazugehörigen Höhe mal genommen
wird.
A = a·ha = b·hb
Aufgabe 1: Bewege die orangen und roten Schieber der Grafik und beobachte, was passiert.
Die orangen und roten Punkte der Grafik sind beweglich.
Aufgabe 2: Wandle das Parallelogramm in ein Rechteck um und trage unten den Flächeninhalt ein. Ein Kästchen ist 1 cm2 groß.
Die Figur hat einen Flächeninhalt von cm2.
richtig: 0falsch: 0
Aufgabe 3: Berechne den Flächeninhalt des Parallelogramms.
Das Parallelogramm hat einen Flächeninhalt von cm2.
richtig: 0falsch: 0
Aufgabe 4: Trage den Umfang und den Flächeninhalt des Parallelogramms unten ein.
u = cm | A = cm²
richtig: 0falsch: 0
Aufgabe 5: Bewege die Punkte auf die angegebenen Koordinaten und berechne den Flächeninhalt.
A(); B(); C(); D()
Der Flächeninhalt beträgt cm².
richtig: 0falsch: 0
Aufgabe 6: Ein Parallelogramm hat einen Umfang von cm. Die Seite a ist cm lang. Wie lang ist die Seite a?
Die Seite a ist cm lang.
richtig: 0falsch: 0
Aufgabe 7: Ein Parallelogramm hat einen Flächeninhalt von cm². Die Seite a ist cm lang. Wie lang ist die Höhe zur Seite a?
Die Höhe zur Seite a ist cm lang.
richtig: 0falsch: 0
Aufgabe 8: Die bräunliche Treppenhausschräge soll getäfelt werden. Der Schreiner berechnet 95,20 € pro m² für das Täfeln. Berechne die Kosten.
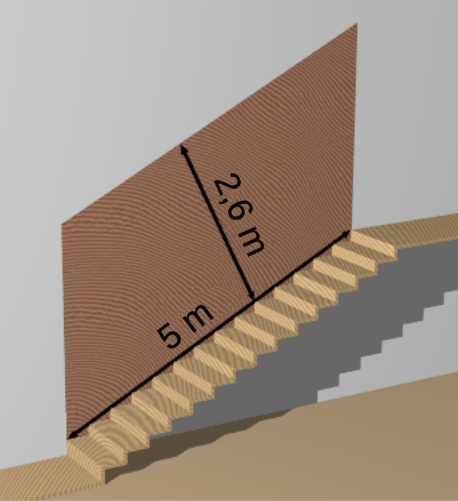
Das Täfeln des Aufgangs kostet €.
Versuche: 0
Aufgabe 9: Trage die fehlenden Werte der Parallelogramme ein.
| Seite a |
Höhe ha |
Fläche A |
|
| a) | cm | cm | cm² |
| b) | cm | cm | cm² |
| c) | dm | dm | dm² |
richtig: 0falsch: 0
Aufgabe 10: Trage unten in die Textfelder die fehlenden Größen ein.
richtig: 0falsch: 0
Aufgabe 11: Trage den Flächeninhalt der folgenden Figur unten ein.

Die Figur hat einen Flächeninhalt von cm2.
Versuche: 0

