Raute
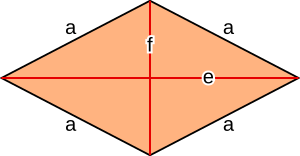
Eine Raute ist ein Viereck mit vier gleich langen Seiten. Gegenüberliegende Seiten sind parallel. Gegenüberliegende Winkel sind gleich groß.
- Der Umfang einer Raute ergibt sich aus der Summe der
vier Seitenlängen.
u = 4a - Der Flächeninhalt einer Raute wird folgendermaßen berechnet:
A = e · f 2
Aufgabe 1: Bewege die orangen Gleiter und beobachte, was passiert.
Die blaue und die grüne Fläche der Raute können so umgelegt werden, dass die graue Rautenfläche zu einem Rechteck ergänzt wird. Dieses Rechteck hat die Länge e und die Breite f 2 . Der Flächeninhalt der Raute ist genauso groß wie der Flächeninhalt des Rechtecks: e · f 2
Aufgabe 2: Trage den Umfang (u) der Rauten mit den gegeben Seitenlängen (a) ein.
| a | u | |
| a) | cm | |
| b) | cm | |
| c) | m |
richtig: 0falsch: 0
Aufgabe 3: Trage die Seitenlängen (a) der Rauten mit dem Umfang (u) ein.
| u | a | |
| a) | cm | |
| b) | cm | |
| c) | m |
richtig: 0falsch: 0
Aufgabe 4: Trage den Flächeninhalt (A) der Rauten mit den gegeben Diagonalenlängen (e, f) ein.
| e | f | A | |
| a) | cm² | ||
| b) | cm² | ||
| c) | m² |
richtig: 0falsch: 0
Aufgabe 5: Trage die fehlenden Diagonallängen (e, f) der Rauten mit dem gegebenen Flächeninhalt (A) ein.
| A | e | f | |
| a) | cm | ||
| b) | cm | ||
| c) | m |
richtig: 0falsch: 0
Aufgabe 6: Die Diagonale (d) eines Quadrates ist lang. Welchen Flächeninhalt hat das Quadrat?
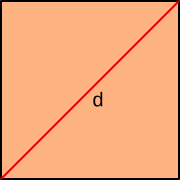
Der Flächeninhalt beträgt cm².
richtig: 0falsch: 0
Drachen
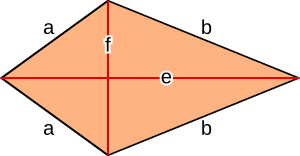
Ein Drachen ist ein Viereck, das zwei Paare gleich lange benachbarte Seiten aufweist. Eine Diagonale (hier e) ist die Symmetrieachse.
- Der Umfang des Drachens ergibt sich aus der Summe der
vier Seitenlängen.
u = 2a + 2b - Der Flächeninhalt eines Drachen wird folgendermaßen berechnet:
A = e · f 2
Aufgabe 7: Bewege die orangen Gleiter und beobachte, was passiert.
Die blaue und die grüne Fläche des Drachen können so umgelegt werden, dass die graue Drachenfläche zu einem Rechteck ergänzt wird. Dieses Rechteck hat die Länge e und die Breite f 2 . Der Flächeninhalt des Drachen ist genauso groß wie der Flächeninhalt des Rechtecks: e · f 2
Aufgabe 8: Trage den Flächeninhalt des symmetrischen Drachens unten ein.
A = cm²
richtig: 0falsch: 0
Aufgabe 9: Bewege die Punkte auf die angegebenen Koordinaten und berechne den Flächeninhalt.
A(); B(); C(); D()
Der Flächeninhalt beträgt cm².
richtig: 0falsch: 0
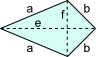 Aufgabe 10: Ein symmetrischer Drachen hat eine Umfang von . Die Seite b ist lang. Wie lang ist die Seite a?
Aufgabe 10: Ein symmetrischer Drachen hat eine Umfang von . Die Seite b ist lang. Wie lang ist die Seite a?
Die Seite a ist cm lang.
richtig: 0falsch: 0

Aufgabe 11: Ein Drachen hat einen Flächeninhalt von cm². Die Seite e ist cm lang. Wie lang ist Seite f?
Die Seite f ist cm lang.
richtig: 0falsch: 0
Aufgabe 12: Trage die fehlenden Werte der Drachen ein.
| Seite e |
Seite f |
Fläche A |
|
| a) | cm | cm | cm² |
| b) | cm | cm | cm² |
| c) | dm | dm | dm² |
richtig: 0falsch: 0

