Winkel 
Ein Winkel entsteht durch die Drehung einer Halbgeraden um einen festen Punkt. Der Ausgangspunkt eines Winkels heißt Scheitel. Die Strahlen eines Winkels heißen Schenkel. Winkel werden mit griechischen Buchstaben bezeichnet: α - Alpha, β - Beta, γ - Gamma ...
![]()
Winkel messen
Aufgabe 1: Mit dem Geodreieck kann man Winkel messen und zeichnen. Der Nullpunkt des Geodreiecks liegt dabei im Scheitel (S) des Winkels. Verändere den Winkel mit dem orangen Gleiter und lies ihn am Geodreieck ab.
Aufgabe 2: Miss mit dem Geodreieck (rot gekreuzte Anfasser) die Winkel und trage die richtigen Angaben unten auf 1° genau ein.
| α = ° | β = ° | γ = ° | δ = ° |
|
|||
Aufgabe 3: Erstelle mit den orangen Gleitern möglichst genau einen Winkel von . Die Aufgabe wird als richtig gewertet, wenn sich dein konstruierter Winkel um höchsten 5° zur Vorgabe unterscheidet.
Dein Winkel:
°
richtig: 0 | falsch: 0
Winkelarten
Aufgabe 4: Bewege die orangen Punkte der Grafik. Es werden unterschiedliche Winkelarten angezeigt. Klick anschließend die unten aufgeführten Winkelart an, die jeweils in den roten Rahmen unter der entsprechenden Gradangabe passt.
| >0° <90° |
90° |
>90° <180° |
180° |
>180° <360° |
360° |
Winkel rechter
Winkel spitzer
Winkel stumpfer
Winkel überstumpfer
Winkel voller
Winkel
Versuche: 0
Aufgabe 5 a: Ordne den Winkeln die richtigen Neben- und Scheitelwinkel zu und trage die richtigen Begriffe ein.
- Nebenwinkel: Winkel, die an kreuzenden Geraden nebeneinander liegen
- Scheitelwinkel: Winkel, die sich an kreuzenden Geraden gegenüber liegen
Versuche: 0 | |||||||||||||||||||||
Aufgabe 5 b: Trage die fehlenden Winkel ein.
| Winkel |
45° | 60° | ° | ° | ° |
| Nebenwinkel |
° | ° | ° | ° | 10° |
| Scheitelwinkel |
° | ° | 30° | 125° | ° |
Versuche: 0
Aufgabe 6 a: Ordne den Winkeln die richtigen Stufen- und Wechselwinkel zu und trage den richtigen Begriff ein.
Zwei parallele Geraden werden von einer dritten Geraden geschnitten.
- Stufenwinkel: Winkel an den Parallelen, die die gleiche Lage haben.
- Wechselwinkel: Winkel an den Parallelen, die die entgegengesetzte Lage haben.
Versuche: 0 | |||||||||||||||||||||||||||||
Aufgabe 6 b: Vervollständige den folgenden Satz richtig:
Der Wechselwinkel ist der winkel des Stufenwinkels.
Versuche: 0
Winkel berechnen
Aufgabe 7: Trage die Größe der Winkel unten ein.
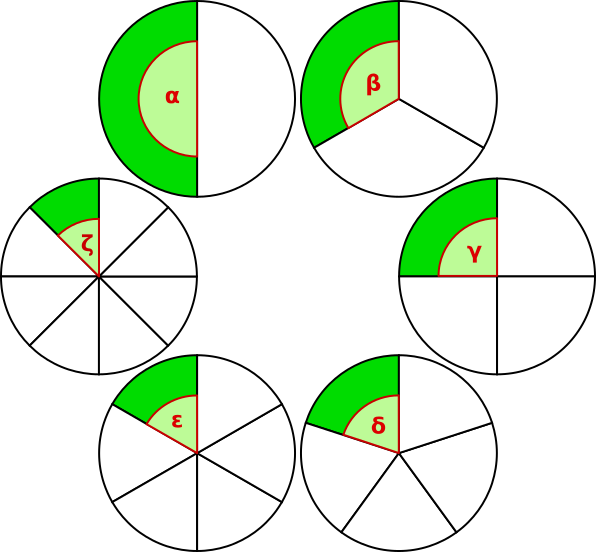
α = °, β = °, γ = °, δ = °, ε = °, ζ = °
Versuche: 0
Aufgabe 8: Trage die Größe der Winkel unten ein.
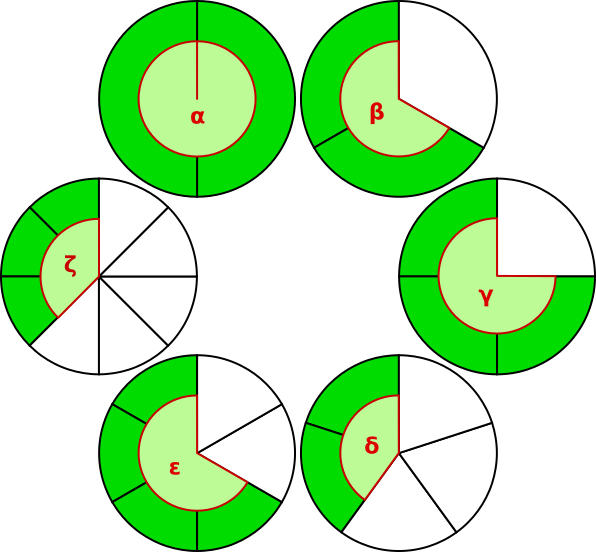
α = °, β = °, γ = °, δ = °, ε = °, ζ = °
Versuche: 0
Aufgabe 9: Trage die Größe der Winkel unten ein.

α = °, β = °, γ = °, δ = °, ε = °, ζ = °
Versuche: 0
Aufgabe 10: Zu welcher vollen Stunde bilden der Minuten- und der Stundenzeiger einer Uhr einen gestreckten Winkel?
Um Uhr bilden beide Zeiger einen gestreckten Winkel.
Versuche: 0
| Aufgabe 11 | a) Eine Wetterfahne zeigt vormittags nach Norden, am Nachmittag dreht sie sich nach Südwesten. Um wieviel Grad drehte sie sich? |
| b) Am nächsten Tag dreht sie sich um 90° gegen den Uhrzeigersinn. In welche Richtung zeigt sie jetzt? |
| a) Die Wetterfahne dreht ich um °. |
| b) Die Wetterfahne zeigt nach . |
Versuche: 0
Aufgabe 12: Trage die Größe von Winkel α ein.
Winkel α ist ° groß.
richtig: 0falsch: 0
Aufgabe 13: Trage die Größe von Winkel α ein.
Winkel α ist ° groß.
richtig: 0falsch: 0
Aufgabe 14: Trage die Größe von Winkel α und β ein.
Winkel α ist ° und Winkel β ° groß.
richtig: 0falsch: 0
Aufgabe 15: Trage die Größe des Winkels δ aus dem Rechteck unten ein.
Der Winkel δ hat eine Größe von °.
richtig: 0falsch: 0
Aufgabe 16: Trage die Größe der Winkel α und β ein.

α = ° | β = °
Versuche: 0
Aufgabe 17: Trage die gesuchten Winkel α und β ein. Die blauen Linien sind parallel.
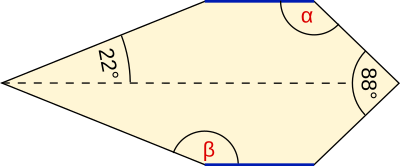
α = β =
Versuche: 0
Aufgabe 18: Winkel β ist dreimal so groß wie Winkel α. Winkel γ ist fünfmal so groß wie Winkel α. Trage die Winkelgrößen unten ein.

α = β = γ =
Versuche: 0
Aufgabe 19: Trage den Winkel α unten ein.

Winkel α beträgt °.
Versuche: 0
Aufgabe 20: Trage die Größe von Winkel α ein.

Winkel α beträgt °.
Versuche: 0
Aufgabe 21: Trage den Winkel α und die farbig markierten Winkel ein. Ein Dreieck hat eine Winkelsumme von 180°.
| β = ° ; γ = ° | |||
| α = ° | rot = ° | blau = ° | grün = ° |
|
richtig: 0falsch: 0 |
|||
Aufgabe 22: Trage die fehlenden Winkel ein.
| a)
6 = ° 4 = ° α = ° β = ° γ = ° |
b) 1 = ° 5 = ° α = ° β = ° γ = ° |
c) 3 = ° α = ° β = ° γ = ° |
d) 2 = ° 5 = ° α = ° β = ° γ = ° |
|
richtig: 0falsch: 0 |
|||
Aufgabe 23: Im Dreieck ABC ist der Winkel γ doppelt so groß wie der Winkel β. Wie groß ist der Winkel α?

Winkel α beträgt °.
Versuche: 0
Aufgabe 24: Trage die fehlenden Winkel ein.
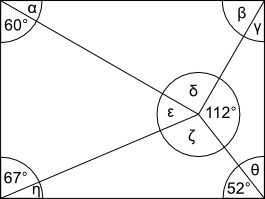
|
||
| α = ° | β = ° | γ = ° |
| δ = ° | ε = ° | ζ = ° |
| η = ° | θ = ° | |
Versuche: 0
Aufgabe 25: Trage die Winkel α und β ein.

α = ° β = °
Versuche: 0
Aufgabe 26 Trage die fehlenden Winkel ein.
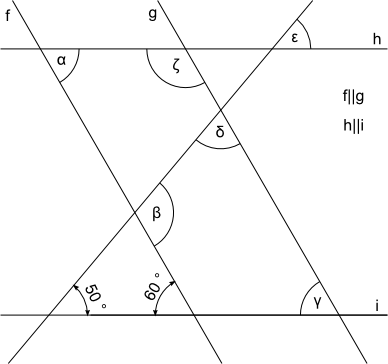
|
||
| α = ° | β = ° | γ = ° |
| δ = ° | ε = ° | ζ = ° |
Versuche: 0
Aufgabe 27: Welchen Winkel schließen Minuten- und Stundenzeiger um Uhr ein? Berücksichtige, dass sich der Stundenzeiger in den verstrichenen Minuten ebenfalls bewegt. Trage den kleineren der entstandenen Winkel ein.
Hilfe: Der Stundenzeiger bewegt sich 2,5° in 5 Minuten.
Die beiden Zeiger stehen in einem Winkel von °.
richtig: 0falsch: 0



