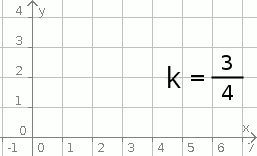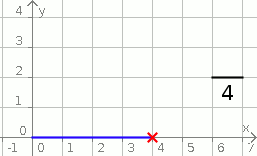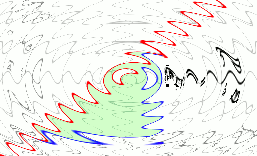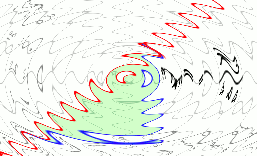Gewertete
Aufgaben:

Aufgaben
mindestens
min
begrenzen
Nr.:
  ↑  

Funktionen - Stil: i

Hier findest du Aufgaben zu folgenden Themenbereichen:

Darstellung

TB-PDF

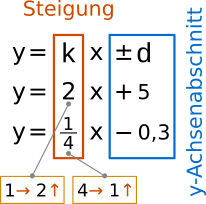
Aufgabe 1: Trage die richtigen Begriffe ein.

Merke dir bitte:
  • Eine Funktion ist eine eindeutige (ordnuZung).
  • Jeder Größe aus dem Definitionsbereich wird genau eine Größe aus dem (berteWereich) zugeordnet.
  • Funktionen können als Formel, als Wertetabelle und als (karfiG) dargestellt werden.
  • In einer Grafik liegen die Werte einer proportionalen Funktion alle auf einer (Gadener), die unendlich viele (kteuPn) hat.
  • Jede Gerade kann durch (weiz) Punkte bestimmt werden.

Versuche: 0


Funktionen können dargestellt werden als ...
Text:

Jedem x-Wert wird ein Viertel seine Wertes zugeordnet.
Schaubild: Schaubild Funktion
Wertetabelle:
x 0 1 2 3 4
y 0 0,25 0,5 0,75 1
Funktionsgleichung:

y = ¼x

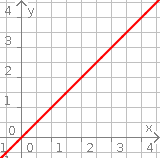
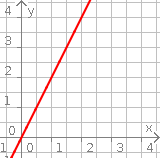
Aufgabe 2: Ergänze die richtigen Daten für die verschiedenen Darstellungsformen der Funktionen.

Text Jedem x-Wert wird seines Wertes zugeordnet. Jedem x-Wert wird seines Wertes zugeordnet. Jedem x-Wert wird seines Wertes zugeordnet.
Schaubild 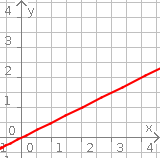Funktion Funktion Funktion
Tabelle
x 0 1 2 3 4
y 0 2
x 0 1 2 3 4
y 0 4
x 0 1 2 3 4
y 0 8
Gleichung

Versuche: 0

Aufgabe 3: Werden einem x-Wert mehrere y-Werte zugeordnet, handelt es sich nicht um eine Funktion. Klick an, ob es sich um Schaubilder einer Funktion handelt oder nicht.

Funktionsvorschriften und Funktionswerte einander zuordnen

Aufgabe 4: Klick an, welche Aussage zu welchem Graph gehört.

A1: Pro Stück bezahlt man 1,50 €.
A2: Ein Haar ist 2 cm lang. Es wächst jeden Monat einen Zentimeter.
A3: Alle drei Stunden tropft ein Liter Wasser aus dem Wasserhahn.

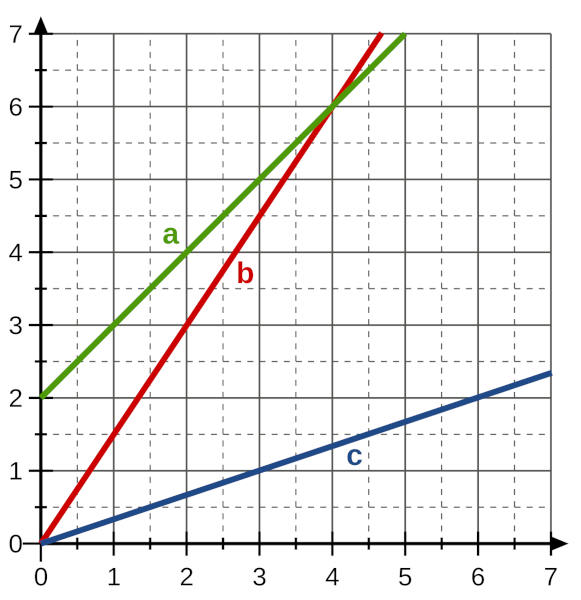
A1 gehört zu Graph
A2 gehört zu Graph
A3 gehört zu Graph

Versuche: 0

Aufgabe 5: Ergänze die fehlenden Werte der dargestellten Funktion in der Wertetabelle und die darunter stehende Gleichung.

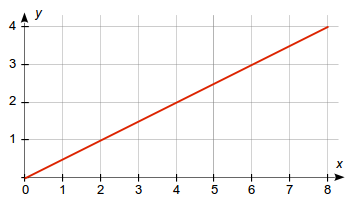
Funktion

x 0 1 2 3 4 5 6 7 8
y 0 0,5 1

Gleichung: y = x

Versuche: 0

Aufgabe 6: Trage die fehlenden y-Werte ein.

a) 

y = 2x
x 0 1 2 3 4
y

b) 

y = x + 3
x 0 1 2 3 4
y

c) 

y = 0,4x
x 0 1 2 3 4
y

d) 

y = 2x + 5
x 0 1 2 3 4
y

Versuche: 0

Aufgabe 7: Ergänze die Gleichungen für folgende Wertetabellen.

a) 

y = x
x 0 1 2 3 4
y 0 3 6 9 12

b) 

y = x
x 0 1 2 3 4
y 0 1,5 3 4,5 6

c) 

y = x
x 0 1 2 3 4
y 0 0,3 0,6 0,9 1,2

d) 

y = x
x 0 1 2 3 4
y 0 2,3 4,6 6,9 9,2

Versuche: 0

Aufgabe 8: Ergänze die Gleichung und trage die fehlenden y-Werte ein.

y = x

x 0 1 2 3 4
y 0


richtig: 0falsch: 0

Aufgabe 9: Ergänze die Gleichung und trage die fehlenden y-Werte ein.

y = x

x 0 1 2 3 4
y 0


richtig: 0falsch: 0

Aufgabe 10: Ergänze die Gleichung und trage die fehlenden y-Werte ein.

y = x

x 0 1 2 3 4
y 0


richtig: 0falsch: 0

Aufgabe 11: Ergänze die jeweilige Funktionsgleichung so, dass sie zur Wertetabelle passt.

Wertetabelle Funktionsgleichung
a) 
kg 1 2 3 4
Preis (€) 1,25 2,50 3,75 5,00
y = x
b) 
kg 10 20 30 40
Preis (€) 14,50 29,00 43,50 58,00
y = x
c) 
kg 5 15 20 25
Preis (€) 9,90 29,70 39,60 49,50
y = x
d) 
kg 6 9 12
Preis (€) 70,20 105,30 140,4
y = x

Versuche: 0

Aufgabe 12: Der Punkt P gehört zum Graphen der Funktion. Trage die fehlenden Werte ein.

a) P(5| ); y = x - 3 b) P(7| ); y = 2x + 1
c) P(6| ); y = 5x - 8 d) P(4| ); y = -x + 7

Versuche: 0

Aufgabe 13: Ergänze die Funktionsgleichung so, dass sie zur Zuordnungsvorschrift passt.

Beispiel:
  • Funktion: Zahl → Doppelter Zahlwert
  • Funktionsgleichung: y = 2x
a)  Zahl → siebenfacher Zahlwert y = x
b)  Zahl → halber Zahlwert y = x
c)  Zahl → um eins verminderte Zahl y = x -
d)  Zahl → um zwei verminderte Zahl y = x -
e)  Zahl → zweieinhalbfacher Zahlwert y = x
f)  Zahl → dreifacher Zahlwert vermindert um fünf y = x -

Versuche: 0

Aufgabe 14: Trage die fehlenden y-Werte ein.

x 0 1 2 3 4 5 6 7 8
y


richtig: 0falsch: 0

Aufgabe 15: Erstelle eine Wertetabelle mit den ganzzahligen x-Werten von 0 bis 4 für die aufgeführten Funktionsgleichungen.

a) y = 2 · (x + 1,5)

x
y

b) y = 1,5 · (x + 1)

x
y

c) y = ½ · (x - 4)

x
y

d) y = 4 · (x+1)

x
y

Versuche: 0

Aufgabe 16: Trage die fehlenden y-Werte ein.

y = x

x 0 1 2 3 4
y


richtig: 0falsch: 0

Proportionale Funktion

Die grafische Darstellung einer proportionalen Funktion ist eine Gerade durch den Nullpunkt (0|0) mit der Steigung m.

Positive Steigung

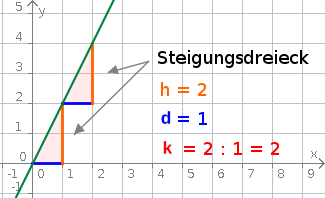
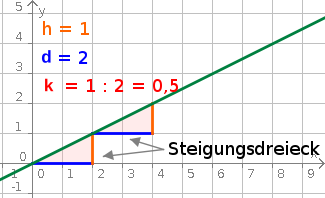
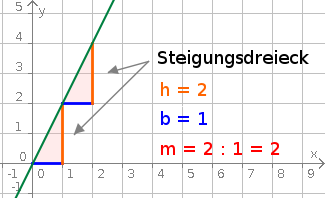
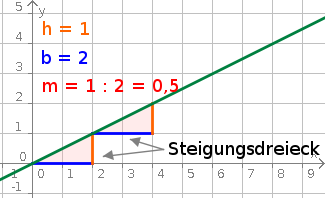
Aufgabe 17: Klick unter der Grafik auf die Steuerungstasten um zu sehen, was mit Steigung gemeint ist.

© 2000 - http://geonext.de

GEONExT
<< <  AUTO  > >>

Legt man an die Gerade ein Steigungsdreieck, lässt sich die Steigung ermitteln, indem die Höhe des Dreiecks durch die Breite des Dreiecks geteilt wird.

m =  Dreieckshöhe in y-Richtung
Dreiecksbreite in x-Richtung

Steigungsdreieck Steigungsdreieck

Die Gleichung einer proportionalen Funktion lautet y = m · x.
(Die Steigung ist der Faktor von x.)

y = 2x

y = ½x

Aufgabe 18: Stelle den orangen Gleiter auf die unten angegebenen Koordinaten und trage die fehlenden Werte für die proportionale Funktion ein.


Die Werte sind gerundet.


Punkt
Koordinate		 Steigung Gleichung
(2|6) m = y = x
(2|5) m = y = x
(6|3) m = y = x
(4|3) m = y = x
(3|6) m = y = x
(4|5) m = y = x

Versuche: 0

Aufgabe 19: Schau dir die Ergebnisse der vorangegangenen Aufgabe an und ziehe die richtigen Werte zur Berechnung der Steigung m in die entsprechenden Felder.

m = 

Versuche: 0

Aufgabe 20: In den Klappmenüs stehen 5 unterschiedliche Funktionsgleichungen. Ordne sie entsprechend der Steilheit der durch sie entstehenden Geraden.

Geradenrangliste
steilste:
zweitsteilste:
drittsteilste:
viertsteilste:
flachste:

Versuche: 0

Aufgabe 21: Gib an, welche unterschiedlichen Steigungen der Fahrradfahrer auf seiner Etappe zu überwinden hat.

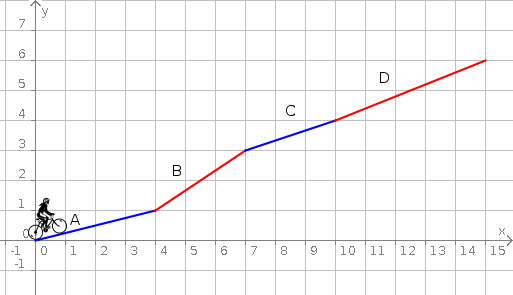
Steigung

A B C D
m =  1
m = 
m = 
m = 

Versuche: 0


Info: Graphen proportionaler Funktionen verlaufen durch den Koordinatenursprung (0|0). Vom Ursprung ausgehend lässt sich mit der Steigung ein zweiter Punkt markieren, den die Gerade der Gleichung streift. Ist die Steigung m = ¾, dann heißt das: Gehe vom Ursprung aus 4 Einheiten nach rechts und 3 Einheiten nach oben. Durch den dort liegenden Punkt wird die Gerade gezogen.

Graph einer proportionale Funktion
(Steigung m = ¾ = 0,75)

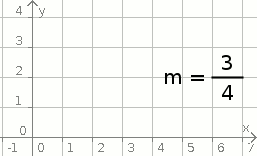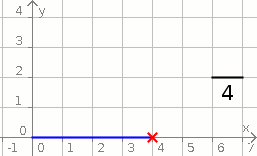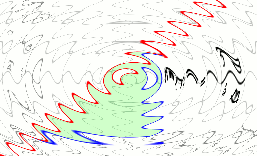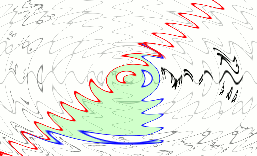
Steigung Beispiel

Aufgabe 22: Zieh die orangen Gleiter so, dass die angegebenen Steigungen entstehen. Wandelst du die Dezimalzahlen in einen Bruch um, erhälst du die geigneten Koordinaten [0,75 = ¾ → P(4|3)].

A B C D E


richtig: 0 | falsch: 0

Aufgabe 23: Trage die fehlenden Koordinaten der Punkte so ein, dass sie zur Funktionsgleichung passen. Die Zeichnung gibt dir einen Hinweis, wie du rechnen kannst.

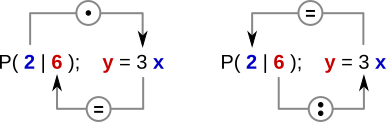
Funktion-Koordinate-Gleichung

a)  P( |); y = x    b)  P( |); y = x
 
c)  P( |); y = x    d)  P( |); y = x


richtig: 0 | falsch: 0

Aufgabe 24: Klick auf die Gleichung, die zu den Koordinaten der rot markierten Punktes passt. Zwölf Punkte sind zuzuordnen.

richtig: 0 | falsch: 0

y=3x

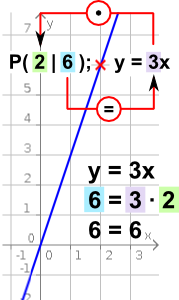
Durch das richtige Einsetzen der Koordinaten eines Punktes in die Funktionsgleichung wird kontrolliert, ob sich der Punkt auf der Geraden der Gleichung befindet. Stimmen beide Seiten der Gleichung nach dem Einsetzen der Koordinaten überein, dann liegt der Punkt auf der Geraden.

Aufgabe 25: Gib an, ob folgende Punkte auf den aufgeführten Geraden liegen.

Gleichung

Punkt

richtig

falsch
a) y = 0,5x P(6|3)
b) y = 3x P(12|4)
c) y =  1 x
4
P(3|12)
d) y = 1,2x P(1|2)
e) y = 2,5x P(4|10)

Negative Steigung

Steigung Gefälle
Steigung Gefälle

Bei einem Gefälle ist die Steigung negativ (kleiner als 0). Eine negative Steigung erkennt man am Minuszeichen vor m: y = -mx.

Aufgabe 26: Zieh die orangen Gleiter so, dass die angegebenen negativen Steigungen entstehen.

A B C D E


richtig: 0 | falsch: 0

Aufgabe 27: Eine Gerade verläuft durch den Koordinatenursprung und jeweils durch den unten angegebenen Punkt. Trage die Steigung der Geraden als Dezimalzahl ein und ergänze entsprechend die Funktionsgleichung.

Punkt Steigung Gleichung   Punkt Steigung Gleichung
a) (3|6) m = y = x b) (-1|3) m = y = x
c) (-4|2) m = y = x d)
( 4 | 1 )
7 7
m = y = x
e) (-3|-12) m = y = x f) (10|1) m = y = x

Versuche: 0

Aufgabe 28: Klick auf den Buchstaben, dessen Graph zur roten Gleichung passt. Acht Gleichungen sind zuzuordnen.

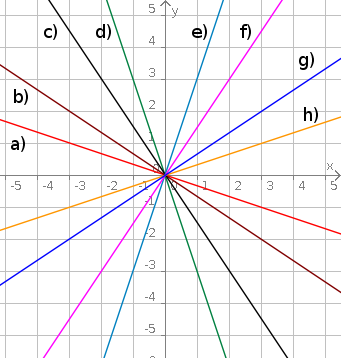
Funktionsgraphen

richtig: 0 | falsch: 0

Aufgabe 29: Zieh die orangen Gleiter so, dass die zugeordnete Gleichung stimmt.

A B C D E


richtig: 0 | falsch: 0

Lineare Funktion (y = mx ± b)

Proportionale Funktionen wie y = mx gehen immer durch den Nullpunkt. Eine lineare Funktion kann die y-Achse auch an einer anderen Stelle als dem Nullpunkt schneiden. Solche Funktionen sind um die Konstante b erweitert: y = mx ± b.

TB-PDF

Aufgabe 30: Trage die richtigen Begriffe ein.

Merke dir bitte:

Steigung und y-Achsenabschnitt
Bei einer linearen Funktion y = mx ± b werden zwei Veränderungsmöglichkeiten unterschieden.

  • Die Veränderung im y- (abschenAchsnitt): Die Konstante b gibt dabei an, bei welchem Punkt die Gerade der Funktion die y-Achse schneidet.

    • Beispiel: y = 2x + 5

    • Die y-Achse schneidet die x-Achse am Punkt x = 0. Daher wird für x = 0 gesetzt.
    • y = 2 · 0 + 5
    • y = b = 5

  • Die Veränderung in der teigSung: Der Faktor m zeigt an, wie steil die Gerade der Funktion verläuft.
    • Ist m ein Bruch, dann zeigt in einem Steigungsdreieck der (ählZer) den "Weg" in y-Richtung und der (renneN) den "Weg" in x-Richtung an.

      • m =  "Weg" in
      "Weg" in

Versuche: 0

Aufgabe 31: Zieh die orangen Gleiter. Du kannst erkennen, dass die Gerade einer linearen Funktion die y-Achse immer an der Konstanten b schneidet.

Aufgabe 32: Trage die zur Gleichung gehörende Steigung m, den y-Achsenabschnitt b sowie die Koordinaten des Schnittpunktes mit der y-Achse Sy ein.

m b Sy
a) y = (|)
b) y = (|)


richtig: 0falsch: 0

Aufgabe 33: Die 5 Geraden sind parallel zueinander. Die rote Gerade c hat die Steigung m = 0,5. Gib die Funktionsgleichungen der jeweiligen Geraden an:

a) y = x

b) y = x + 2

c) y = x

d) y = x

e) y = x

Versuche: 0

Parallele Geraden

TB-PDF

Aufgabe 34: Trage die richtigen Begriffe ein.

Merke dir bitte:

Eine Funktion kannst du mit folgenden Methoden in ein Koordinatensystem einzeichnen:

  • Du erstellst eine Welletaberte (x, y) und überträgst die jeweiligen tunPke ins Koordinatensystem. Durch die Punkte ziehst du eine erGade.
  • Du fügst zuerst den y- schnittsenAchab ein. Von diesem Punkt aus gelangst du mithilfe der geiStung ("Weg" in x- und y-Richtung ) zu einem zweiten Punkt. Durch diese zwei Punkte ziehst du eine radeGe.
    • Ist die Steigung eine ganze Zahl, gibt sie den "Weg" in y-Richtung an. Der "Weg" für die x-Richtung ist 1.
    • Ist die Steigung ein Bruch, gibt der hälZer den "Weg" in y-Richtung und der renneN den Weg in x-Richtung an.

Versuche: 0

Aufgabe 35: Zeichne die Funktion der mittleren Spalte mit Hilfe der Gleiter. Nach der Auswertung wird rechts daneben eingeblendet, was für eine Funktion du gezeichnet hast.

Funktion


richtig: 0 | falsch: 0

Aufgabe 36: Ziehe die roten Gleiter so, dass die Gerade zu folgender Funktionsgleichung passt:


richtig: 0 | falsch: 0

Aufgabe 37: Ergänze die Funktionsgleichung. Benutze die Form y = mx + b (y = mx; y = b).

Beispiel: m = 2; b = 1; Gleichung: y = 2x + 1

m b Gleichung
y =
y =


richtig: 0falsch: 0

Aufgabe 38: Gib die Funktionsgleichung der Geraden an, die die y-Achse in Punkt P schneiden und die Steigung m haben. Benutze die Form y = mx + b (y = mx; y = b).

Beispiel: m = 2; P = (0|1); Gleichung: y = 2x + 1

m P Gleichung
(0|) y =
(0|) y =


richtig: 0falsch: 0

Aufgabe 39: Gib die Funktionsgleichung der Geraden an, die die y-Achse in Punkt P schneiden und die Steigung m haben.

Punkt Steigung Gleichung   Punkt Steigung Gleichung
a) (0|1) m = 2 y = x b) (0|-4)
m =  3
2
y = x
c) (0|-5) m = -3 y = x d) (0|1,5) m = -2 y = x
e) (0|-7)
m =  3
4
y = x f) (0|-0,5) m = -2,5 y = x

Versuche: 0

Aufgabe 40: Vergegenwärtige dir durch das Ziehen der orangen Gleiter nochmals, wie du aus einem Schaubild die jeweilige Funktionsgleichung ermitteln kannst.

  • Stelle die Steigung (m) fest.
    Wenn du von einem Punkt der Geraden einen Schritt nach rechts gehst, wie viele Schritte musst du anschließend noch oben (+) oder nach unten (-) gehen, um wieder auf die Gerade zu gelangen?
  • Stelle den Schnittpunkt an der y-Achse (b) fest.
  • Setze Steigung (m) und Schnittpunkt (b) in die Gleichung y = mx + b ein.

TB-PDF

Aufgabe 41: Trage die richtigen Begriffe ein.

Merke dir bitte:

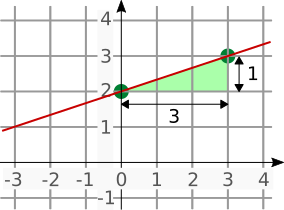Um aus einem Schaubild die Funktion zu ermitteln, gehst du folgendermaßen vor:

  • Bestimme zuerst den y- (absenAchschnitt). Hier: b = 2
  • Bestimme einen weiteren - gut ablesbaren - (kunPt). Hier: P(3|3)
  • Zeichne das (deigungsreiSteck) ein.
  • Lese vom Steigungsdreieck die (reckenStlängen) ab. Hier: 3→ 1↑
  • Setze die abgelesenen Werte in die (feigungsStormel) ein.
    Hier: m = 1 3
  • Setze die (tunkiFon) zusammen.
    Hier: y =  1 3 x + 2

Versuche: 0

Aufgabe 42: Gib die Funktionsgleichungen für die abgebildeten Geraden an.

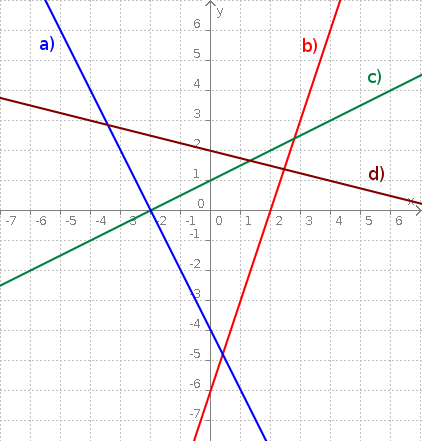
Funktionsgraphen

a) y = x - b) y = x -
c) y = x + d) y = x +

Versuche: 0

Aufgabe 43: Gib die Funktionsgleichungen für die abgebildeten Geraden in der Form y =  x  an.

a) y = x     b) y = x     c) y = x 


richtig: 0falsch: 0

Aufgabe 44: Stelle die Funktionsgleichungen so um, dass die der Form y = mx + b entsprechen. Trage die jeweilige Steigung (m) und den y-Achsenabschnitt (b) ein.

y = mx + bmb
a) y = +- b +- mx y = x
b) y +- mx = +- b y = x
c) y +- b = +- mx y = x
d) +- mx + y +- b = 0 y = x
e) ny +- nb = +- nmx y = x
f) +- nmx + ny +-n b = 0 y = x


richtig: 0falsch: 0

Aufgabe 45: Klick an, ob der Graph der roten Gleichung parallel zum Graph der blauen Gleichung liegt oder nicht.

y = 3x + 5

richtig: 0 | falsch: 0

Punktprobe

Mit der Punktprobe findest du heraus, ob ein bestimmter Punkt auf einer vorgegebenen Geraden mit der Funktionsgleichung y = mx + b liegt. Dafür setzt du die x- und die y-Koordinate des entsprechenden Punktes in die Gleichung ein.

Beispiel:

Gleichung:  y = 5x - 3
Punkte:  P1(1|2) P2(2|1)
Rechnung:  2 = 5 · 1 - 3
2 = 5 - 3
2 = 2		 1 = 2 · 5 - 3
1 = 10 - 3
1 ≠ 7
Ergebnis:  P1 liegt auf
der Geraden.		 P2 liegt nicht auf
der Geraden.

Aufgabe 46: Ergänze die unteren Punktangaben so, dass der Punkt auf der durch die Funktionsgleichung bestimmten Geraden liegt.


richtig: 0falsch: 0

Aufgabe 47: Gegeben sind die lineare Funktion und der Geradenpunkt . Bestimme b.

b =


richtig: 0falsch: 0

Aufgabe 48: Gegeben sind die lineare Funktion und der Geradenpunkt . Bestimme m.

m =


richtig: 0falsch: 0

Aufgabe 49: Trage die lineare Funktion zu der Geraden ein, die durch den Punkt geht und parallel zur Geraden verläuft.

y =


richtig: 0falsch: 0

Aufgabe 50: Zwei Grundstücke werden durch einen Zaun voneinander abgegrenzt. Die 13 Zaunpfosten stehen in einem Abstand von 3 Metern. Der Zaun soll erneuert werden. Beim neuen Zaun haben die Pfosten eine Entfernung von 2,40 m zueinander. Wie viele Pfosten werden für den neuen Zaun benötigt? (Eine Skizze ist hilfreich.)

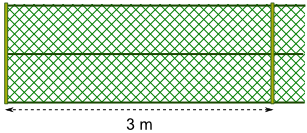
Zaunfeld

Antwort: Für den neuen Zaun werden Pfosten benötigt.

Versuche: 0

Aufgabe 51: Ein Schwimmbecken wird mit Wasser gefüllt. In jeder Stunde steigt der Wasserspiegel um 0,4 m. Die Wasserhöhe des gefüllten Beckens beträgt 2,5 m. Nach wie vielen Stunden ist das Becken gefüllt?

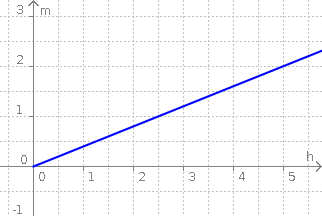
Pegel

Antwort: Das Becken ist nach Stunden gefüllt.

Versuche: 0

Aufgabe 52: Frank wandert pro Stunde 5 km. Eine halbe Stunde später fährt Tom den gleichen Weg mit 15 km/h. Nach wie vielen Kilometern überholt er Frank? Runde auf 2 Nachkommastellen.

Weg - Zeit

Antwort: Tom überholt Frank nach km.

Versuche: 0

Funktionsgleichung rechnend aus zwei Punkten ermitteln

Um die Funktionsgleichung einer linearen Funktion rechnerisch aus zwei ihre Punkte A(x1|y1 ) und B(x2|y2 ) zu bestimmen, benötigt man die Steigung m und den y-Achsenabschnitt b.

m Die Steigung wird durch die Steigungsformel berechnet: Steigungsformel
b Der y-Achsenabschnitt b wird mit der Funktionsgleichung y = mx + b bestimmt.
Die berechnete Steigung (m) und ein Koordinatenpunkt (z.B. A) wird in die Gleichung eingesetzt.
Die Gleichung wird nach b hin aufgelöst: b = y1 - m · x1

Beispiel

Wie lautet die Funktionsgleichung, deren Gerade durch die Punkte A(-2|3) und B(4|6) verläuft?
1. Steigung berechnen: Funktionsgleichung
2. y-Achsenabschnitt berechnen:  b = y1 - m · x1 = 3 - ½ · (-2) = 4
3. Funktionsgleichung aufstellen: y = ½x + 4

Aufgabe 53: Die Punkte A und B bestimmen die Gerade g. Ermittle die Steigung m, den y-Achsenabschnitt b und die Funktionsgleichung von g.

Steigung:  m =
y-Achsenabschnitt:  b =
Funktionsgleichung:  y = x


richtig: 0falsch: 0

Aufgabe 54: Eine Gerade verläuft durch den Punkt A und hat den Steigungsfaktor m = . Ermittle den y-Achsenabschnitt b und die Funktionsgleichung von g.

y-Achsenabschnitt:  b =
Funktionsgleichung:  y = x


richtig: 0falsch: 0

Aufgabe 55: Die Punkte A und B bestimmen die Gerade g. Ermittle die Funktionsgleichung von g und den Punkt, an dem g die x-Achse schneidet.

Funktionsgleichung:  y = x
Schnittpunkt der x-Achse:  P = (| 0 )


richtig: 0falsch: 0

Aufgabe 56: Die Punkte A und B bestimmen die Gerade g. Der Punkt C() befindet sich ebenfalls auf g. Ermittle die Funktionsgleichung von g und die -Koordinate von C.

Funktionsgleichung:  y = x
-Koordinate:  C = ()


richtig: 0falsch: 0

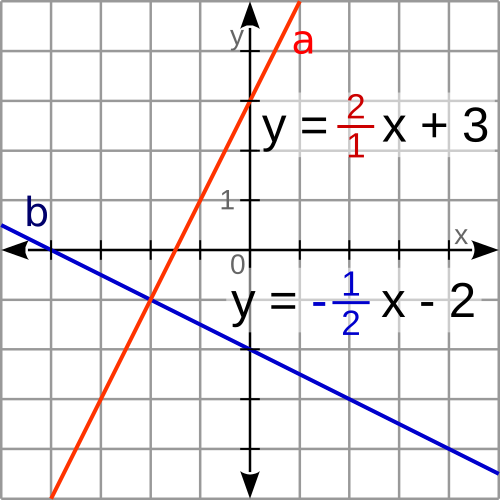Senkrechte Geraden Eine Gerade (a) steht senkrecht zu einer anderen Geraden (b), wenn die eine Steigung der negative Kehrwert der anderen Steigung ist. Im Beispiel hat die Gerade a die Steigung m = 2 und die Gerade b die Steigung m = -½. Beide Geraden stehen senkrecht zueinander.

Aufgabe 57: Die Punkte A und B bestimmen die Gerade g1. Im Punkt C() schneidet eine weitere Gerade g2 die Gerade g1 senkrecht. Trage die Funktionsgleichung von g1 und g2 ein. Verwende für den Eintrag Dezimalzahlen

Funktionsgleichung g1:  y = x
Funktionsgleichung g2:  y = x


richtig: 0falsch: 0
Danke | Datenschutz | Fehlerinfo | Impressum | Sitemap