Gleichungen mit einer Unbekannten
Beim Lösen einer Geichungen mit einer Unbekannten (a,b,...n,m...x,y...) geht es darum, den Wert dieser Unbekannten herauszufinden.
Hier kannst du ...
- Denksportaufgaben durchführen (A 1 - A 4),
- erfahren, wie Gleichungen gelöst werden,
- Einfache Gleichungen (A 5 - A 32),
- Gleichungen mit Klammern (A 33 - A 41),
- Textaufgaben mit Fachbegriffen (A 42 - A 61),
- Aufgaben aus der Geometrie (A 62 - A 70)
- und Sachaufgaben lösen (A 71 - A 88).
Denksportaufgaben: Spiel mit Gleichungen
Aufgabe 1: Klick auf einen Beispiel-Buchstaben und berechne die Aufgabe. Findest du den Trick heraus?

|
Beispiel | Term |
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
Aufgabe 2: Trage unten ein, wie groß x bei einer ausgeglichenen Waage ist.
a) Ganze Zahlen: | b) Kommazahlen:
|
X
X
X
X
X
X
X
X
X
X
Y
Y
Y
Y
Y
Y
|
x =
a) richtig: 0 | falsch: 0
b) richtig: 0 | falsch: 0
Aufgabe 3: Ein Mobile hängt im Gleichgewicht. Trage das Gewicht der unten dargestellten Teile ein.
| a)
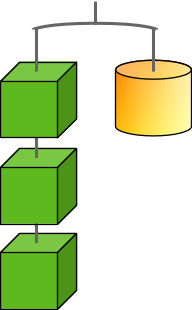 |
b)
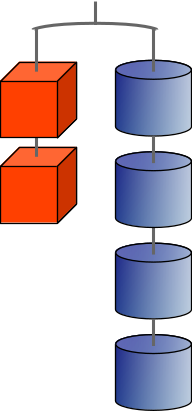 |
c)
 |
richtig: 0falsch: 0
Aufgabe 4: Ein Mobile hängt im Gleichgewicht. Trage das Gewicht der unten dargestellten Teile ein.
| a)
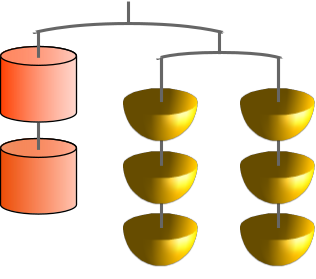 |
b)
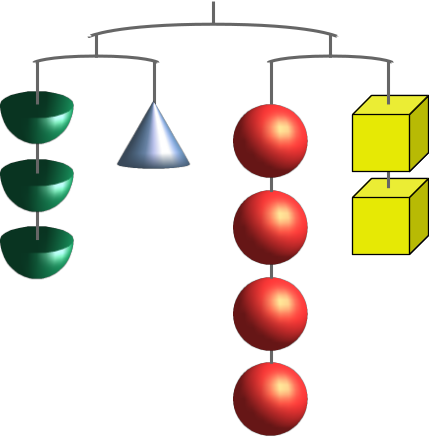 |
|
|
richtig: 0falsch: 0
Gleichungen lösen (Äquivalenzumformungen)
Beim Lösen einer Geichungen mit einer Unbekannten (x) geht es darum, diese Unbekannte (x) herauszufinden. Als Trick stellt man sich dazu eine Gleichung als Waage vor. Das "Gewicht" beider Waagschalen wird so verändert, dass sich am Ende nur noch x auf der einen und die Lösungszahl auf der anderen Waagschale befindet. Ist die Waage in diesem Moment im Gleichgewicht, hat man die Lösung.
Beispiel
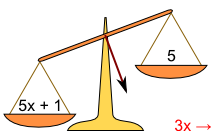
| Ich stelle mir die Gleichung 5x + 1 = 3x + 5 auf einer Waage vor. | |||

Durch Umformen möchte ich erreichen, dass zum Schluss x auf einer Seite und eine Zahl auf der anderen Seite steht. |
|||
| Die Unbekannten sollen nur noch auf einer Waagschale sein. | |||
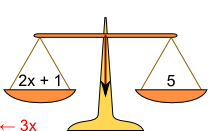
| a) | Ich ziehe die 3x auf der rechten Seite ab. | b) | Ich ziehe 3x auch links ab, um das Gleichgewicht wieder herzustellen. |
 |
 |
||
| Jetzt sollen die Unbekannten alleine stehen. | |||
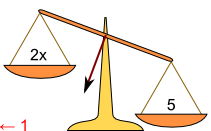
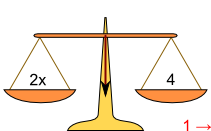
| c) | Ich ziehe die 1 auf der linken Seite ab. | d) | Ich ziehe die 1 auch rechts ab, um das Gleichgewicht wieder herzustellen. |
 |
 |
||
| Nur eine einzige Unbekannte soll übrig bleiben. | |||
| e) | Ich teile die linke Seite durch 2. | f) | Ich teile auch die rechte Seite durch 2, um das Gleichgewicht wieder herzustellen. |
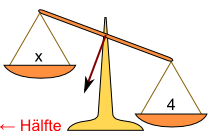 |
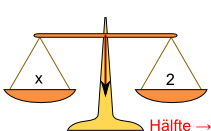 |
||
| Ich kann jetzt ablesen: x = 2. | |||
Einfache Gleichungen
Aufgabe 5: Berechne die Länge der Seite x und y.
| a) |
|
|||||
| b) |
|
|||||
|
cm + cm = x x - cm = cm x - cm = cm |
cm - cm = y cm + y = cm cm - y = cm |
|||||
|
x = cm y = cm richtig: 0falsch: 0 |
||||||
Aufgabe 6: Trage die richtigen Werte ein.
| a) 0 + = | b) + = |
| c) 0 + = | d) + = |
| e) 0 - = | f) - = |
| g) 0 - = | h) - = |
richtig: 0falsch: 0
Aufgabe 7: Berechne x aus -x.
Erscheint ein -x als Ergebnis einer Gleichung, stellt sich die Frage: "Wie kommst du von -x zu x?" Eine Möglichkeit ist die Multiplikation beider Gleichungsseiten mit (-1).
Beispiele:
|
|
| a) | -x = 34 | b) | -x = -34 |
| x = | x = | ||
| c) | 34 = -x | d) | -34 = -x |
| x = | x = | ||
richtig: 0falsch: 0
Aufgabe 8: Berechne x.
|
|||||
| a) | x = | b) | x = | ||
| c) | x = | d) | x = | ||
richtig: 0falsch: 0
Aufgabe 9: Klick an, ob das x im rote Term ¼, ½ oder ¾ entspricht. Neun Terme sind zuzuordnen.
richtig: 0 | falsch: 0
Aufgabe 10: Stelle für die unten abgebildete Waage ein Gleichgewicht her, indem du den passenden Wert für y einträgst.
75 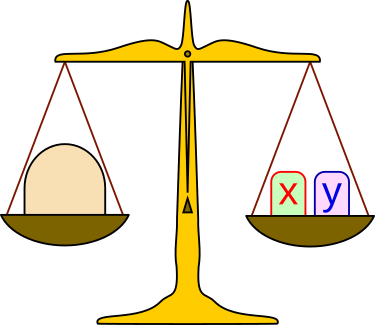 |
| a) | x hat den Wert . y = |
| b) | x ist so groß wie y. y = |
richtig: 0falsch: 0
Aufgabe 11: Berechne die Länge einer Teilstrecke x.
x = cm |
x = cm |
|
richtig: 0falsch: 0 |
Aufgabe 12: Trage die richtigen Werte ein.
| a) 0 · = | b) · = |
| c) 0 · = | d) · = |
| e) 0 : = | f) : = |
| g) 0 : = | h) : = |
richtig: 0falsch: 0
Aufgabe 13: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 14: Berechne die Länge der Strecke x.
| Angabe in cm | |||
x : a = b cm | |||
x = cm | |||
|
richtig: 0falsch: 0 |
Aufgabe 15: Berechne die Länge der Strecke x.
| Angabe in cm | |||
x : a · b = c cm | |||
x = cm | |||
|
richtig: 0falsch: 0 |
Aufgabe 16: Berechne x
|
x = | ||||||
|
x = | ||||||
| c) 1,5x = 24 | x = |
richtig: 0falsch: 0
Aufgabe 17: Berechne x
|
x = | |||||
|
x = |
richtig: 0falsch: 0
Aufgabe 18: Berechne die Länge einer Teilstrecke x.
|
x + cm = cm cm - x = cm |
x = cm |
|
richtig: 0falsch: 0 |
Aufgabe 19: Berechne x.
|
|||||
| a) | x = | b) | x = | ||
| c) | x = | d) | x = | ||
|
|||||
Aufgabe 20: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 21: Berechne x
| a) = | x = |
| b) = | x = |
| c) = | x = |
richtig: 0falsch: 0
Aufgabe 22: Berechne x
|
x = | |||||
|
x = | |||||
|
x = |
richtig: 0falsch: 0
Aufgabe 23: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 24: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 25: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 26: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 27: Trage in die Textfelder die Zahlen ein, mit denen beide Seiten der unteren Waage verändert werden sollen. Klick auf "Los", um die Veränderung durchzuführen.
|
Ursprüngliche Gleichung: |
||||||||||

|
Rechenschritte für beide Waagschaalen:
|
Aufgabe 28: Berechne die Länge einer Teilstrecke x.
|
x + cm = x + cm |
x = cm |
|
richtig: 0falsch: 0 |
Aufgabe 29: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
| d) -2x = -4 | x = |
richtig: 0falsch: 0
Aufgabe 30: Berechne x
x =
richtig: 0falsch: 0
Aufgabe 31: Berechne x
| a) 15x - 23 = 8x : 2 + 10 | x = | |
| b) 17x - 19 = 13x + 17 - 2x | x = | |
| c) 12x - 7 = 10x - 7 | x = |
Versuche: 0
Aufgabe 32: Berechne x
| a) 2x = 4 | x = |
| b) -2x = 4 | x = |
| c) 2x = -4 | x = |
richtig: 0falsch: 0
Gleichungen mit Klammern
Umformen
Gleichungen löst man durch Umformen. Zum Schluss steht die Variable allein auf der einen und die Lösung auf der anderen Seite des Gleichheitszeichens.
Auf beiden Gleichungsseiten darf
- dieselbe Zahl addiert oder multipliziert werden.
- mit derselben Zahl (außer 0) multipliziert oder durch sie dividiert werden.
Beispiel
|
a) Klammer auflösen b) Zusammenfassen |
2y - (2 + 4y) 2y - 2 - 4y |
= = |
32 - 2 (4y - 4)
32 - 8y + 8 |
| Ka | zf |
|
c) Variable einseitig d) Variable allein e) Variable berechnen |
-2 - 2y -2 + 6y 6y y |
= = = = |
-8y + 40 40 42 7 |
| +8y
| +2 | :6 |
Aufgabe 33: Klick im Klappmenü den gewünschten Aufgabentyp an. Berechne den farbig markierten Term und füge in das gleichfarbige Textfeld die Lösung ein.
|
Keine negative Variable |
Hilfe in
sec
|
|||
| Klammer auflösen | x | = | ||
| Zusammenfassen | x | = | ||
| Variable einseitig | x | = | ||
| Variable allein | x | = | ||
| Variable berechnen | x | = | ||
| x | = | |||
Aufgabe 34: Berechne x
| a) | x = |
| b) | x = |
| c) | x = |
| d) | x = |
richtig: 0falsch: 0
Aufgabe 35: Berechne x
| a) | x = |
| b) | x = |
| c) | x = |
| d) | x = |
richtig: 0falsch: 0
Aufgabe 36: Berechne x
| a) xx | x = |
| b) xx | x = |
richtig: 0falsch: 0
Aufgabe 37: Berechne x
| a) | x = |
| b) | x = |
| c) | x = |
| d) | x = |
richtig: 0falsch: 0
Aufgabe 38: Berechne x
| a) | x = |
| b) | x = |
| c) | x = |
| d) | x = |
richtig: 0falsch: 0
Aufgabe 39: Berechne x
| a) 4,5 · (x + 2) = 27 + 3,5x | x = | |
| b) -5 · (12 - 3x) = 4x + 17 | x = | |
| c) -5x = (x - 13,5) · 4 | x = | |
| d) 4 · (2x - 12) = -18,5x + 5 | x = |
Versuche: 0
Aufgabe 40: Berechne x
| a) xx | x = |
| b) xx | x = |
richtig: 0falsch: 0
Aufgabe 41: Berechne x
|
x = | ||||||||||
|
x = | ||||||||||
|
x = | ||||||||||
|
x = |
Versuche: 0
Aufgabe 42: Stelle zum Text eine Gleichung auf und berechne x.
| a) | Multipliziere eine Zahl x mit 4, addiere die Zahl 10. Du erhälst 22. | x = |
| b) | Multipliziere eine Zahl x mit 7, addiere die Zahl 4. Du erhälst 60 | x = |
| c) | Multipliziere eine Zahl x mit 11, subtrahiere die Zahl 21. Du erhälst 111. | x = |
richtig: 0falsch: 0
Aufgabe 43: Trage die richtigen Werte der Unbekannten (v, w, x, y, z) ein.
| a) Die Hälfte von v ist 21. | v = | |
| b) Das 3-fache von w ist 48. | w = | |
| c) Das 4-fache von x plus 4 ist 56. | x = | |
| d) Ein Drittel von y minus 3 ist 9. | y = | |
| e) Ein Fünftel von z mal 4 ist 32. | z = |
richtig: 0falsch: 0
Aufgabe 44: einer Zahl x, erhält man das von x.
x =
richtig: 0falsch: 0
Aufgabe 45: Vermindert man um das einer Zahl x, erhält man wieder x.
x =
richtig: 0falsch: 0
Aufgabe 46: Addiert man zum einer Zahl x ihr , erhält man .
x =
richtig: 0falsch: 0
Aufgabe 47: Der dritte Teil einer Zahl ist um 2 größer als der vierte Teil.
Es handelt sich um die Zahl .
Versuche: 0
Aufgabe 48: Stelle zum Text eine Gleichung auf und berechne x.
| a) | Nimm eine Zahl x und subtrahiere 6. Dein Ergebnis ist gleich 36 minus dem fünffachen deiner gesuchten Zahl. | x = |
| b) | Multipliziere deine gesuchte Zahl x mit der Zahl 3 und teile das Ergebnis durch 4. Dann ist das Ergebnis gleich deine gesuchte Zahl minus 2. | x = |
| c) | Subtrahiere das dreifache einer gesuchten Zahl x von 12 und du erhälst 18 vermindert um das vierfache deiner Zahl. | x = |
Versuche: 0
Aufgabe 49: Addiert man zu einer Zahl (x) die beiden darauffolgenden Zahlen (, ) so erhält man die Zahl 444. Trage den Wert der jeweiligen Zahl unten ein.
x = y = z =
Versuche: 0
Aufgabe 50: Subtrahiert man vom 10-fachen einer Zahl x, so erhält man das der Zahl.
x =
richtig: 0falsch: 0
Aufgabe 51: Die Summe aus dem , dem und dem einer Zahl x ergibt .
x =
richtig: 0falsch: 0
Aufgabe 52: Die Summe aus der Hälfte und dem Drittel einer Zahl x ist .
x =
richtig: 0falsch: 0
Aufgabe 53: Vermindert man das einer Zahl x um ihren dritten Teil, so erhält man .
x =
richtig: 0falsch: 0
Aufgabe 54: Das einer um vergrößerten Zahl x ist .
x =
richtig: 0falsch: 0
Aufgabe 55: Das einer um vermehrten Zahl x ist gleich der Hälfte von .
x =
richtig: 0falsch: 0
Aufgabe 56: Die Summe zweier aufeinander folgender Zahlen ist . Welchen Wert hat die kleinere der beiden Zahlen?
Die kleinere Zahl hat den Wert .
richtig: 0falsch: 0
Aufgabe 57: Zerlege die Zahl so in zwei Summanden, dass der zweite Summand um größer ist als der erste Summand.
Summand 1 = Summand 2 =
richtig: 0falsch: 0
Aufgabe 58: Trage die richtigen Werte der Unbekannten (v, w, x, y, z) ein.
| a) Wenn ich die Hälfte von 4 mal 9 nehme, dann ist v noch um 3 mal 5 kleiner. | v = | |
| b) Wenn ich 3 mal 9 zu w addiere, dann habe ich 4 mal 8. | w = | |
| c) Wenn ich 3 mal 7 verdopple, dann habe ich die Häfte von x. | x = | |
| d) Wenn ich 4 mal 3 von y subtrahiere, dann habe ich die Hälfte von 6 mal 7 | y = | |
| e) Wenn ich ein Drittel von 51 zu z addiere, dann habe ich 6 mal 7. | z = |
Versuche: 0
Aufgabe 59: Gegeben sei eine Zahl. Dividiert man die Summe aus dieser Zahl und 11 durch vier, so erhält man dasselbe wie wenn man die Differenz von dieser Zahl und 11 mit 3 multipliziert.
Es handelt sich um die Zahl .
Versuche: 0
Aufgabe 60: Zählt man vom einer Zahl x um zurück, so gelangt man zur selben Zahl, wie wenn man vom der Zahl um weiterzählt.
x =
richtig: 0falsch: 0
Aufgabe 61: Multipliziert man die Differenz aus dem Zwölffachen einer Zahl x und 8 mit drei Viertel und subtrahiert vom Ergebnis die Summe aus der Zahl und 15, so erhält man die Hälfte der Summe aus dem Fünffachen der Zahl und 15,2.
x =
Versuche: 0
Aufgabe 62: Trage die fehlenden Winkel ein. Die Winkelsumme in einem Dreieck beträgt 180°.
 |
|||
| a) x = ° | b) x = ° | c) x = ° | d) x = ° |
Versuche: 0
Aufgabe 63: Trage die fehlenden Winkel ein.
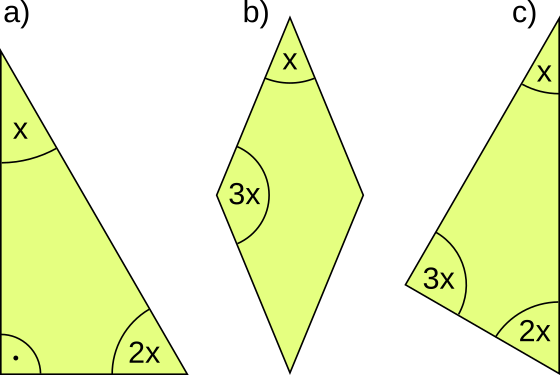 |
|||
| a) x = ° | b) x = ° | c) x = ° | |
Versuche: 0
Aufgabe 64: Jede der folgenden Formen hat einen Umfang von cm. Welche Längen haben die Strecken a, b, c und d?

Streckenlänge a: cm, b: cm, c: cm, d: cm
richtig: 0falsch: 0
Aufgabe 65: Der Umfang aller 4 Figuren beträgt 36 cm. Wie lang ist die jeweilige Seite x?
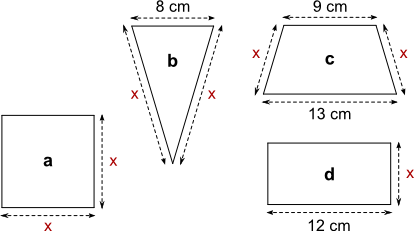 |
|||
| a) x = cm | b) x = cm | c) x = cm | d) x = cm |
Versuche: 0
Aufgabe 66: Die gesamte Kantenlänge von jedem der drei Körper beträgt 96 cm. Wie lang ist die jeweilige Kante x?
 |
||
| a) x = cm | b) x = cm | c) x = cm |
Versuche: 0
Aufgabe 67: Der Umfang aller 4 Figuren beträgt 60 cm. Wie lang ist die jeweilige Seite x?
 |
|||
| a) x = cm | b) x = cm | c) x = cm | d) x = cm |
Versuche: 0
Aufgabe 68: Die Länge eines Rechtecks ist 7 cm größer als seine Breite. Der Umfang des Rechtecks beträgt 50 cm. Wie groß sind die einzelnen Seiten?
Das Rechteck hat eine Länge von cm und eine Breite von cm.
richtig: 0falsch: 0
Aufgabe 69: Die beiden Flächen sind gleich groß. Berechne x.
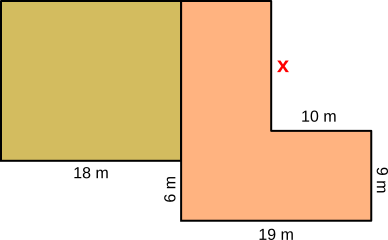
x = m
Versuche: 0
Aufgabe 70: Der Umfang eines Dreiecks beträgt 55 cm. Seite a ist um 8 cm länger als Seite b. Seite c ist um 12 cm kürzer als Seite a. Trage die jeweiligen Seitenlängen ein.
a = cm | b = cm | c = cm
richtig: 0falsch: 0
Aufgabe 71: 340 kg Erbsen werden in 1-kg-, 2,5-kg- und 5-kg-Beuteln verpackt. Wie viele Beutel erhält man, wenn von jeder Sorte gleich viele Beutel gefüllt werden sollen?
Von jeder Packungsgröße werden Beutel gefüllt.
Versuche: 0
Aufgabe 72: Anja erhält 5 € mehr Taschengeld als Luisa; zusammen sind es 35 €. Wie viel Geld erhält jedes Mädchen? Stelle zum Text eine Gleichung auf und berechne das Ergebnis.
|
Anja bekommt € Taschengeld. Luisas Taschengeld beträgt €. |
Versuche: 0
Aufgabe 73: Hannah geht mit ihren Freundinnen Mia und Laura shoppen. Zusammen geben sie 200 € aus. Mia gibt doppelt soviel aus wie Hannah. Laura zahlt 35 € weniger als Mia. Welchen Betrag geben die Freundinnen jeweils aus?
Hannah gibt €, Mia € und Laura € aus.
Versuche: 0
Aufgabe 74: Eine Wandergruppe macht einen zweitägigen Ausflug ins Allgäu. Am zweiten Tag wandert sie 7 km mehr als am ersten Tag. Insgesamt wandert sie 39 km. Wie viel Kilometer legt sie jeden Tag zurück? Stelle zum Text eine Gleichung auf und berechne das Ergebnis.
|
Am ersten Tag wandert die Gruppe km. Am zweiten Tag wandert die Gruppe km. |
Versuche: 0
Aufgabe 75: Bei der Fahrt in die Ferien hat Familie Sommer am ersten Tag die Hälfte der gesamten Strecke zurückgelegt. Als sie am zweiten Tag 145 km gefahren sind, stellt Melissa fest, dass sie noch genau ein Drittel der Gesamtstrecke fahren müssen. Wie lang ist die gesamte Strecke?
Insgesamt legt Familie Sommer eine Strecke von km zurück.
Versuche: 0
Aufgabe 76: Eine Viertelstunde nachdem ein Bus von der Autobahn-Raststätte losgefahren ist, fährt ihm ein Pkw nach. Der Bus fährt mit 90 km/h, der PKW mit 120 km/h. Wie viele Minuten dauert es, bis der PKW den Bus eingeholt hat? Der PKW braucht x Stunden (h).
 |
|
||||||||||
| Fahrzeit bis Treffpunkt | ¼h + xh | xh | |||||||||
| Vorsprung |
|
--- | |||||||||
| gemeinsame Strecke |
|
|
|||||||||
| Treffpunkt |
|
|
Es dauert min bis der PKW den Bus eingeholt hat.
Versuche: 0
Aufgabe 77: Daniela ist 8 Jahre älter als ihr Bruder. Zusammen sind sie 40 Jahre alt. Wie alt sind die Geschwister?
Daniela ist Jahre und ihr Bruder Jahre alt.
Versuche: 0
Aufgabe 78: Can sagt: "Oma ist 52 Jahre älter als ich, also ist sie fünfmal so alt wie ich." Wie alt sind Can und seine Oma? Stelle zum Text eine Gleichung auf und berechne das Ergebnis.
Can ist Jahre und Oma ist Jahre alt.
Versuche: 0
Aufgabe 79: Kira und ihre Eltern sind zusammen 100 Jahre alt. Ihre Mutter ist dreimal so alt wie Kira und zwei Jahre jünger als Kiras Vater. Wie alt ist jeder? Stelle zum Text eine Gleichung auf und berechne das Ergebnis.
|
Kira ist , ihre Mutter und ihr Vater Jahre alt.
Versuche: 0
Aufgabe 80: Lea sagt: "Mein Bruder Ben und ich sind zusammen 25 Jahre alt. Vor 5 Jahren war ich 1½-mal so alt wie Ben." Wie alt sind Lea und Ben? Stelle zum Text eine Gleichung auf und berechne das Ergebnis.
| Alter | Lea | Ben |
| heute | x | 25 - x |
| vor 5 Jahren | x - 5 | 25 - x - 5 |
| Lea war 1½-mal so alt wie Ben. | ||
Lea ist heute Jahre und Ben Jahre alt.
Versuche: 0
Aufgabe 81: Herr Huber und sein Sohn Florian sind heute zusammen 60 Jahre alt. Vor 8 Jahren war der Vater 10 mal so alt wie sein Sohn. Wie alt sind beide?
Florian ist heute Jahre und sein Vater Jahre alt.
Versuche: 0

Aufgabe 82: Frau Dobler ist neunmal so alt wie ihr Enkel. In fünf Jahren sind beide zusammen 90 Jahre alt. Wie alt sind beide?
Frau Dobler ist heute Jahre und ihr Enkel Jahre alt.
Versuche: 0
Aufgabe 83: Frau Keller ist heute viermal so alt wie ihre Tochter. In fünf Jahren wird sie nur noch dreimal so alt sein. Wie alt sind beide?
Frau Keller ist heute Jahre und ihre Tochter Jahre alt.
Versuche: 0
Aufgabe 84: Als Herr Schulze nach seinem Alter gefragt wurde, antwortete er: "6 Jahre habe ich eine glückliche Kindheit verbracht. 1 4 meines Lebens ging ich zur Schule. 3 Jahre lang habe ich studiert und 9 16 meines Lebens bin ich nun schon als Mathelehrer tätig." Wie alt ist er?
Herr Schulze ist Jahre alt.
Versuche: 0
Aufgabe 85: Anton baut einen Turm, der doppelt so hoch ist wie der Turm von Berta. Cäsars Turm ist 20 cm kleiner als der von Berta. Alle Türme übereinandergestellt wären 1 m hoch. Wie hoch ist jeder Turm?
|
Antwort: Antons Turm ist cm hoch. Bertas Turm ist cm hoch. Cäsars Turm ist cm hoch. |
Versuche: 0
Aufgabe 86: Zwei verschieden dicke Kerzen werden zeitgleich angezündet. Die dicke Kerze ist 20 cm hoch und verkürzt sich je Stunde um 25 mm. Die dünne Kerze ist 26 cm hoch und verkürzt sich je Stunde um 33 mm. Nach wie vielen Stunden sind beide Kerzen gleich lang.
Nach Stunden haben beide Kerzen die gleiche Länge.
Versuche: 0
Aufgabe 87: 100 l Marmelade werden in ½-l-Gläser und in 1-l-Gläser abgefüllt. Wie viele Gläser werden von jeder Sorte benötigt, wenn von den 1-l-Gläsern doppelt so viele gefüllt werden sollen wie von den ½-l-Gläsern?

| 100 l | |
| x · ½ l | 2x · 1 l |
Es werden ½-Liter-Gläser und 1-Liter-Gläser gefüllt.
Versuche: 0
Aufgabe 88: Rektor Essig erhält für einen neuen Kopierer im Lehrerzimmer folgende beiden Angebote. Angenommen, es würde nur schwarz-weiß oder nur farbig kopiert werden?
| a) | Bei welcher Anzahl ausschließlicher monatlicher Schwarz-weiß-Kopien ist der Preis für beide Geräte gleich hoch? |
| b) | Bei welcher Anzahl ausschließlicher monatlicher Farbkopien ist der Preis für beide Geräte gleich hoch? |
| Modell | Tischgerät | Standgerät | ||
 |
 |
|||
| Einmalige Anschaffungskosten | 399,00 € | 399,00 € | ||
| Grundpreis monatlich | 17,50 €/mtl. | 44,50 €/mtl. | ||
| Monatliche Freiseiten | SW - Zähler | 500 | 500 | |
| Monatliche Freiseiten | Farbzähler | 0 | 100 | |
| Preis Folgeseite | SW - Zähler | 0,01 € | 0,008 € | |
| Preis Folgeseite | Farbzähler | 0,07 € | 0,054 € | |
| a) | Wenn nur schwarz-weiß kopiert wird, dann ist der Preis bei monatlichen Kopien für beide Geräte gleich hoch? |
| b) | Wenn nur farbig kopiert wird, dann ist der Preis bei monatlichen Kopien für beide Geräte gleich hoch? |
Versuche: 0




