Zusammengesetzte Körper
Um das Volumen und die Oberfläche eines zusammengesetzten Körpers berechnen zu können, muss dieser gedanklich in bekannte Teilkörper zerlegt werden.
Aufgabe 1: Ordne die Körpernamen und die Grundflächen der Teilkörper richtig zu. Klick dazu unten die Begriffe an, die in den rote umrandeten Rahmen gehören.
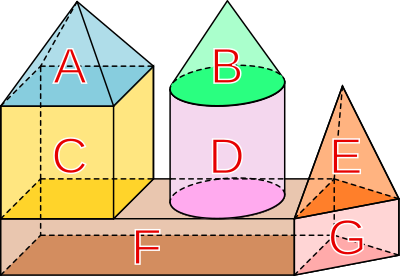
| Körpername | Grundfläche | |
| A) | ||
| B) | ||
| C) | ||
| D) | ||
| E) | ||
| F) | ||
| G) |
Versuche: 0
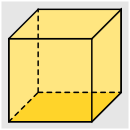
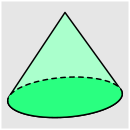
Aufgabe 2: Ordne die Körper der für sie zutreffenden Volumenformel zu.
Volumenformel |
|||||
| Grundfläche · Höhe | |||||
|
|||||

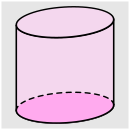
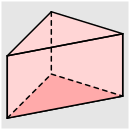
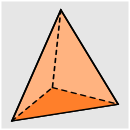
Versuche: 0
Körper mit prismenartigen Elementen
Aufgabe 3 a: Trage das Volumen der Körper in dm3 ein.
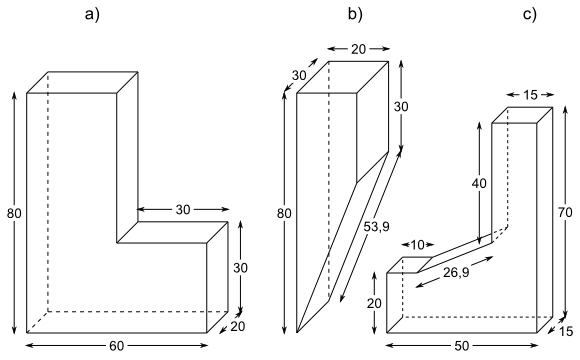
(Maße in cm)
a) V = dm3 b) V = dm3 c) V = ,125 dm3
Versuche: 0
Aufgabe 3 b: Gib die Oberfläche der oberen Körper in m2 an. Runde auf 2 Stellen nach dem Komma.
a) O = m2 b) O = m2 c) O = m2
Versuche: 0
Aufgabe 4: Trage das Volumen und die Oberfläche des folgenden Werkstücks ein. Gib alle Nachkommastellen an.

(Maße in cm)
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 5: Das Bild zeigt das Profil eines Stahlträgers. Der Träger ist 3 m lang. Trage das Volumen und das Gewicht des Trägers unten ein. (1 cm3 Stahl wiegt 7,9 g.)
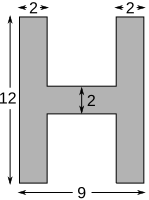
(Maße in cm)
|
a) Volumen = cm3 Versuche: 0 |
b) Gewicht = kg Versuche: 0 |
Aufgabe 6: Der folgende Körper besteht aus einem Quader und einem Dreiecksprisma. Trage das Volumen ein.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 7: Berechne das Volumen und das Gewicht der abgebildeten Mamorstufe. (1 Mamorwürfel mit 10 cm Kantenlänge wiegt 2,7 kg.)
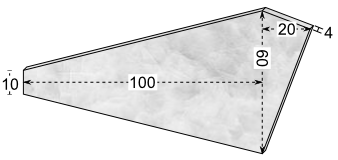
(Maße in cm)
|
a) Volumen = cm3 Versuche: 0 |
b) Gewicht = kg Versuche: 0 |
Aufgabe 8: Das folgende Prisma besteht aus einem Quader mit quadratischer Grundfläche und einem Trapezprisma. Trage das Volumen ein. Runde es auf eine Nachkommastelle.
Das Prisma hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 9: Berechne für das Messingwerkstück das Gewicht auf das Zehntelgramm genau. (1 cm3 wiegt 8,1 g.)
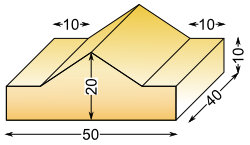
(Maße in mm)
Gewicht = g
Versuche: 0
Aufgabe 10: Ein Schwimmbecken hat die unten angegebenen Maße. Wie viel m³ Wasser passen in dieses Becken hinein?
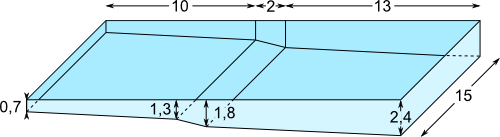
(Maße in m)
Es passen m³ Wasser in das Schwimmbecken hinein.
Versuche: 0
Aufgabe 11: Berechne das Volumen des Kantenmodels eines Würfels. Die Kanten haben einen quadratischen Querschnitt. Vermeide Doppelberechnungen.

Das Kantenmodell hat ein Volumen von cm³.
Versuche: 0
Aufgabe 12: Das folgende Werkstück ist aus Stahl mit einer Dichte von 7,9 g/cm³. Trage das Volumen und das Gewicht ein. Runde das Gewicht auf eine Nachkommastelle. Achte auf die Einheiten!
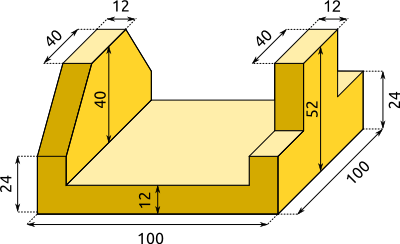
(Maße in mm)
Das Werkstück hat ein Volumen von cm³ und wiegt kg.
Versuche: 0
Aufgabe 13: Ein Würfel mit einer Kantenlänge a von wird so zersägt, dass als neue Fläche ein gleichseitiges Sechseck entsteht. Welchen Flächeninhalt hat dieses Sechseck? Trage den ganzzahligen Teil des Ergebnisses ein. Der Satz des Pythagoras hilft dir beim Lösen.
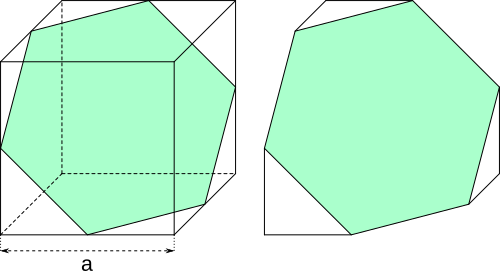
Der Flächeninhalt des Sechsecks beträgt , cm²
richtig: 0falsch: 0
Körper mit zylinderartigen Elementen
Aufgabe 14: Der folgende Körper besteht aus zwei Zylindern. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 15: Trage das Volumen und die Oberfläche des folgende Werkstücks ein. Runde auf ganze cm3 bzw. cm2.
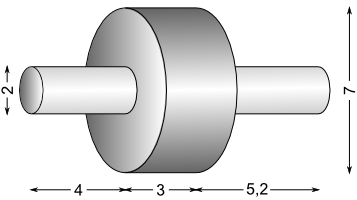
(Maße in cm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 16: Trage das Volumen und die Oberfläche des folgenden Werkstücks ein. Runde auf ganze cm3 bzw. cm2.
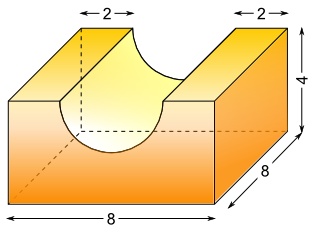
(Maße in cm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 17: Trage den ganzzahligen Wert des Volumens und der Oberfläche des folgenden Gegenstandes ein.
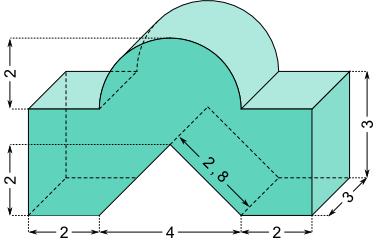
(Maße in cm)
|
a) V = ,85 cm3 Versuche: 0 |
b) O = ,22 cm2 Versuche: 0 |
Aufgabe 18: Aus dem unteren, großen Würfel mit einer Kantenlänge von wurden an jeder Seiten unterschiedliche Prismen heraus gefräst. Die Prismenschnitte befinden sich exakt auf den Kanten und Ecken der kleinen Würfel, die alle gleich groß sind. Welches Volumen hat der gesamte Körper? Runde das Ergebnis auf eine Nachkommastelle
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Körper mit pyramiden- und kegelartigen Elementen
Aufgabe 19: Der folgende Körper besteht aus einer quadratischen Pyramide und einem Quader. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 20: Aus einem Quader mit einer quadratischen Grundfläche wurde eine Pyramide ausgehöhlt. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 21: Trage das Volumen und die Oberfläche des Pfeils ein. Runde auf ganze cm3 bzw. cm2. Achte auf die Einheiten.
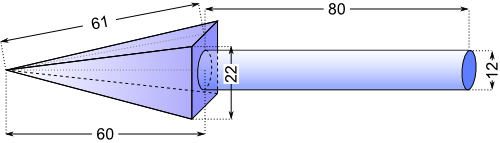
(Maße in mm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 22: Ein Würfel und eine Pyramide sind zu einem Spielzeughaus zusammengeklebt. Trage das Volumen und die Oberfläche des Spielzeugs ein. Für die Berechnung der Oberfläche muss die Dreieckshöhe (?) noch ermittelt werden. Runde auf ganze mm3 bzw. mm2.
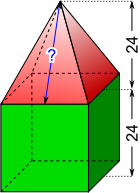
(Maße in mm)
|
a) V = mm3 Versuche: 0 |
b) O = mm2 Versuche: 0 |
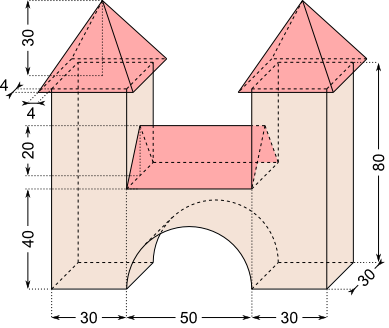
Aufgabe 23: Trage die fehlenden ganzzahligen Werte für das Volumen des folgenden Körpers ein. Beachte die Maßeinheit.
- Die Turmdächer ragen an allen Seiten gleich weit über die jeweilige Wand hinaus.
|
|
|||||||||||||||
Aufgabe 24: Der folgende Körper besteht aus zwei quadratischen Pyramiden. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 25: Auf einer auf dem Kopf stehenden Pyramide ist ein Kreuzgestell aus einem in seiner Mitte befindlichen Quader (6 mm x 6 mm x 30 mm) und vier gleichartigen Prismen befestigt. Berechne das Volumen des Körpers. Beachte die Maßeinheit.
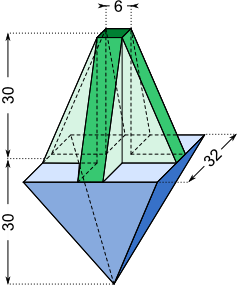
(Maße in mm)
V = cm³
Versuche: 0
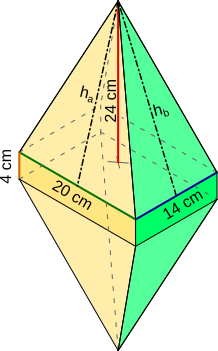
Aufgabe 26: Zwei gleiche Pyramiden mit einer Höhe h = 24 cm werden an ihren rechteckigen Grundflächen (a = 20 cm, b = 14 cm) mit einem passenden Quader (20 cm · 14 cm; Höhe c = 4 cm) verbunden, sodass eine Doppelpyramide entsteht, die in ihrer Mitte über den rechteckigen Quader verbunden ist. Trage unten die ganzzahligen Werte ein.
| a1) | Wie groß ist das Volumen V dieses Körpers? |
| a2) | Wie groß ist der Oberflächeninhalt dieses Körpers? |
| Wie groß ist der Rest-Oberflächeninhalt dieses Körpers, der ... | |
| b1) | senkrecht zu den von den Seitenhöhen hb aufgespannten Fläche halbiert wird? |
| b2) | senkrecht zu den von den Seitenhöhen ha aufgespannten Fläche halbiert wird? |
| b3) | senkrecht zu den von zwei Diagonalen aufgespannten Flächen der rechteckigen Quaderfläche halbiert wird? |
| b4) | senkrecht zur Mitte der rechteckigen Grundfläche halbiert wird? |
 |
| Volumen und Oberflächeninhalt des ganzen Körpers | |
| a1) V = cm³ | a2) O = cm² |
Versuche: 0 |
|
| Jeweiliger Rest-Oberflächeninhalt | |
| b1) O = cm² | b2) O = cm² |
| b3) O = ,57 cm² | b4) O = cm² |
Versuche: 0
Aufgabe 27: Eine ehemals quadratische Pyramide mit eine Grundfläche von 200 mm x 200 mm wird halbiert. Die Hälften werden auf die Schnittfläche gelegt und mit ihren jeweiligen Grundflächen an einem Quader (200 mm x 100 mm x 25 mm) neu verklebt. Welches Volumen und welche Oberfläche hat der neu entstandene Körper? Achte auf die Einheiten.
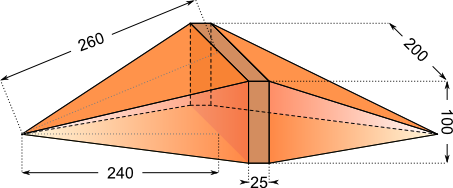
(Maße in mm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 28: Zwei Dreiecksprismen kreuzen sich so, dass die unteren Kanten dieses zusammengesetzten Körpers und seine Höhe die gleiche Länge (a) aufweisen. Welches Volumen hat dieser Körper, wenn a lang ist?
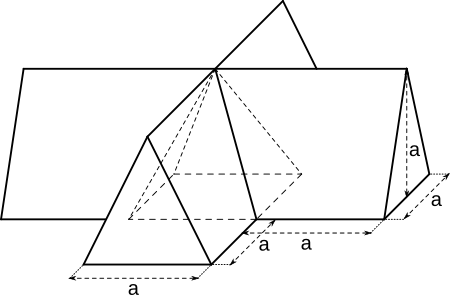
Das Volumen beträgt cm3.
richtig: 0falsch: 0
Aufgabe 29: In einem Aquarium von 15 m Länge, 10 m Breite und 6 m Höhe befinden sich 4 bogenförmige Einbuchtungen, um die Fische besser beobachten zu können. Jede Einbuchtung ist 3 m breit und ragt 2 m tief in das Aquarium hinein. Die Halbkreisbögen spannen sich in 1,5 m Entfernung vom Boden über die Einbuchtungen. Ins Aquarium werden 750 000 Liter Wasser eingelassen. Wie hoch steht das Wasser danach? Runde auf den Zentimeter genau.

Der Wasserpegel befindet sich in m Höhe.
Versuche: 0
Aufgabe 30: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein.
- Zur Berechnung des Volumens muss die Höhe der inneren Pyramide über den Satz des Pythagoras berechnet werden.
- Zur Berechnung der Oberfläche muss bei der Pyramide auch die Höhe des vorderen und hinteren Dreiecks der Mantelfläche ermittelt werden. Die innere Pyramide ist nicht quadratisch.
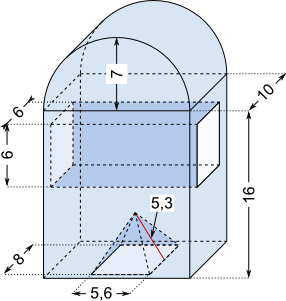
(Maße in cm)
|
a) V = ,49 cm3 Versuche: 0 |
b) O = ,17 cm2 Versuche: 0 |
Aufgabe 31: Der folgende Körper besteht aus einem Kegel und einem Zylinder. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 32: Der folgende Stahlkegel hat eine quadratische Pyramide als Aushöhlung. Stahl hat eine Dichte von 7,9 g/cm³. Trage den ganzzahligen Wert des Gewichts dieses Werkstücks ein?

(Maße in cm)
Gewicht = ,425 kg
Versuche: 0
Aufgabe 33: Trage das Volumen des folgenden Werkstücks ein. Runde auf ganze cm3.
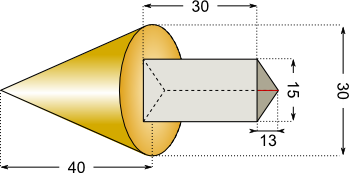
(Maße in cm)
V = cm3
Versuche: 0
Aufgabe 34: Trage das Volumen und die Oberfläche des folgenden Werkstücks ein. Runde auf ganze cm3 bzw. cm2.
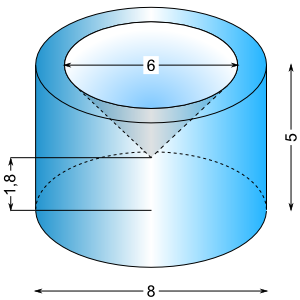
(Maße in cm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 35: Wenn die zusammengesetzten Fläche sich um die rote Achse drehen, entstehen Drehkörper. Trage die jeweiligen ganzzahligen Werte der Volumen ein.

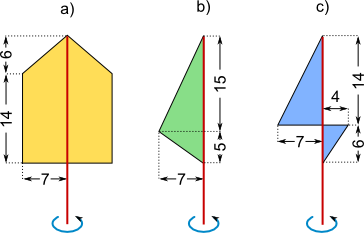
(Maße in cm)
Va = ,01 cm3 Vb = ,25 cm3 Vc = ,91 cm3
Versuche: 0
Aufgabe 36: Der folgende Körper besteht aus zwei Kegeln. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 37: Das folgende Senklot ist aus Messing gefertigt (Dichte 8,48 g/cm³). Wie viel Gramm wiegt es? Runde auf ganze Gramm.
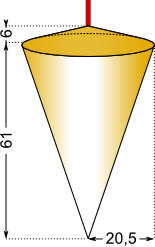
(Maße in mm)
Antwort: Das Senklot wiegt g.
Versuche: 0
Aufgabe 38: Trage das Volumen und die Oberfläche des folgenden Kreisels ein. Runde auf ganze cm3 bzw. cm2.

(Maße in mm)
|
a) V = cm3 Versuche: 0 |
b) O = cm2 Versuche: 0 |
Aufgabe 39: Auf einen Zylinder mit r = 4 cm und h = 15 cm wird ein Kegel mit r = 4 cm und h = 5 cm aufgesetzt. Trage das Volumen des zusammengesetzten Körpers ein. Runde auf ganze cm³.
V = cm³
Versuche: 0
Aufgabe 40: Ein Getreidesilo besteht aus einem 8 m hohen Zylinder und einem 3 m hohen Kegel. Der Radius beträgt 3,10 m. Im Silo befinden sich 151 m³ Getreide. Wie hoch steht das Getreide im Silo? Runde auf ganze Meter.
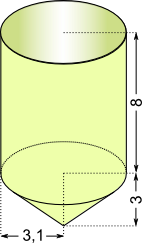
(Maße in m)
Das Getreide steht m über der unteren Siloöffnung.
Versuche: 0
Aufgabe 41: Der folgende Körper besteht aus einer quadratischen Pyramide und einem Quader. Trage das Volumen ein. Ermittle die fehlende Größe mit dem Satz des Pythagoras. Runde auf ganze Kubikdezimeter.
Der Körper hat ein Volumen von dm³.
richtig: 0falsch: 0
Aufgabe 42: Einem Würfel wird auf jeder Seite eine Pyramide mit gleicher Kantenlänge aufgesetzt. Die Höhe der sechs Pyramide beträgt ein Viertel der Kantenlängen. Welches Volumen hat dieser Körper, wenn die Kantenlänge des Würfels cm beträgt?
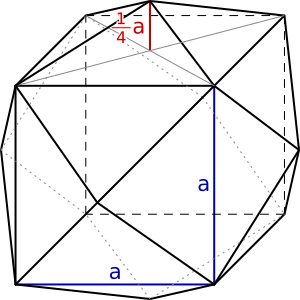
Der Körper hat ein Volumen von cm³
richtig: 0falsch: 0
Aufgabe 43: Der folgende Körper besteht aus einem Kegel und einem Zylinder. Trage den ganzzahligen Wert des Volumens ein. Ermittle die fehlende Größe mit dem Satz des Pythagoras.
Der Körper hat ein Volumen von , cm³.
richtig: 0falsch: 0
Aufgabe 44: Ein Körper besteht aus einem Zylinder und einem aufgesetzten Kegel mit gleichem Durchmesser. Der Kegel hat ein Volumen von 36 dm³ und eine Höhe von 22 cm. Die Zylinderhöhe (hZ) und die Seitenlinie des Kegels (s) sind gleich lang. Wie lang ist die Strecke (x) zwischen der unteren Außenkante des Zylinders bis zur oberen Spitze des Kegels? Runde auf Zentimeter.
Die Strecke ist cm lang.
Versuche: 0
Körper mit kugelartigen Elementen
Aufgabe 45: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein. Achte auf die Einheiten.
(Maße in mm)
|
a) V = ,15 cm3 Versuche: 0 |
b) O = ,50 cm2 Versuche: 0 |
Aufgabe 46: Aus einem Specksteinwürfel wird die größtmögliche Kugel erstellt. Wie viel Abfall fällt dabei an? Runde auf ganze cm3.
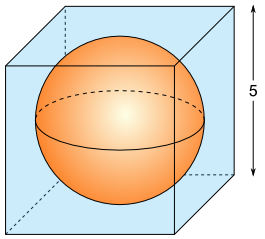
(Maße in cm)
Abfall = cm3
Versuche: 0
Aufgabe 47: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein. Achte auf die Einheiten.
(Maße in mm)
|
a) V = ,15 cm3 Versuche: 0 |
b) O = ,31 cm2 Versuche: 0 |
Aufgabe 48: Ein 60 cm langer Eisenstab mit quadratischer Grundfläche (a = 3 cm) wird zu einem Rundstab mit möglichst großem Durchmesser verarbeitet. Trage das Volumen des Eisenstabes und das Volumen des Rundstabes ein. Runde auf ganze cm3.
V Eisenstab = cm 3 V Rundstab = cm 3
Versuche: 0
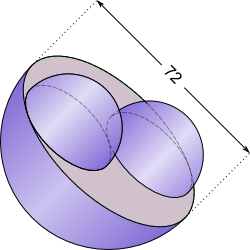
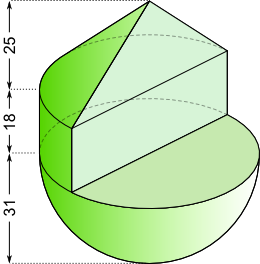
Aufgabe 49: Berechne Volumen und Oberflächeninhalt des folgenden Körpers. Der Radius des kleinen, kugelförmigen Bereichs in der Mitte beträgt 5 cm. Der Radius des großen, umliegenden, kugelförmigen Bereichs beträgt 10 cm. Die gelben Flächen stehen in einem 90° Winkel zueinander. Ihre geraden Kanten peilen genau den Mittelpunkt an. Runde auf eine Nachkommastelle.
| O = cm²
|
V = cm³
|
Aufgabe 50: Berechne a) das Volumen und b) den Oberflächeninhalt des folgenden aus einer Halbkugel, einem Zylinder und einem Kegel zusammengesetzten Körpers. Die eingezeichneten Strecken haben die unten aufgeführten Größen. Runde das Ergebnis auf ganze Kubik- und Quadratzentimeter.
a = | b = | c = | d =
| a) V = cm³ | b) O = cm² | |
|
|
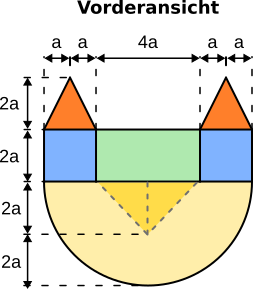
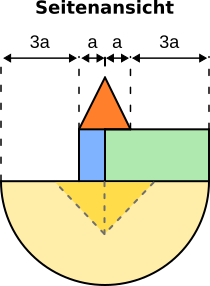
Aufgabe 51: Berechne a) das Volumen und b) den Oberflächeninhalt des folgenden Körpers mit a = cm. Trage den jeweils fehlenden ganzzahligen Wert ein.
 |
 |
 |
|
| V = cm³
|
O = cm²
|
Körper mit pyramidenstumpf- und kegelstumpfartigen Elementen
Aufgabe 52: Der folgende Körper besteht aus einer quadratischen Pyramidenstumpf und einem Quader. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 53: Der folgende Körper besteht aus einer quadratischen Pyramidenstumpf und einem Prisma. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 54: Der folgende Körper besteht aus einem Kegelstumpf und einem Zylinder. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 55: Ein Werkstück besteht aus Kupfer. 1 cm³ Kupfer wiegt 8,96 g. Trage den ganzzahligen Kilogrammwert des Gewichts dieses Werkstücks ein.
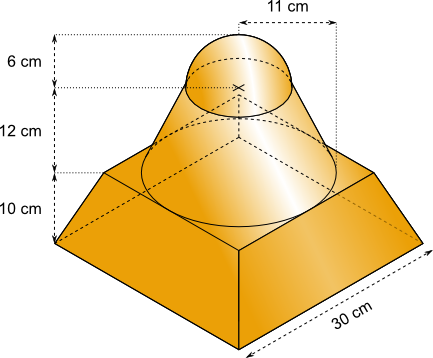
Gewicht = ,2 kg.
Versuche: 0
Aufgabe 56: Eine Bronzeschale besteht aus einem Zylinder und einem Kegelstumpf. Sie hat eine halbkugelförmige Mulde. Trage das Gewicht der Schale ein. Runde auf ganze Gramm. (Dichte von Bronze: 8,8 g/cm³)
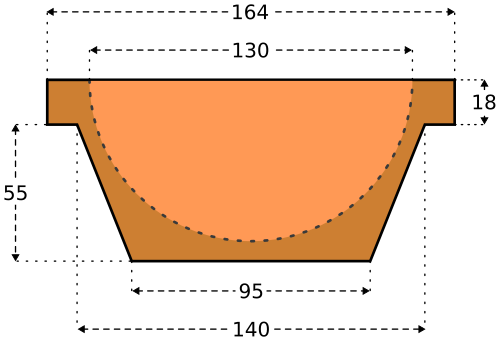 (Maße in mm) |
Gewicht = g.
Versuche: 0
Aufgabe 57: Berechne zuerst das Volumen der einzelnen Teilkörper. Achte beim Eintragen auf die bereits vorhandenen Ziffern. Berechne mit den gerundeten Werten das Volumen des zusammengesetzten Körpers. (Kegelstumpf aus dem der Kegel und die Halbkugel herausgefräst sind.)
Versuche: 0 |
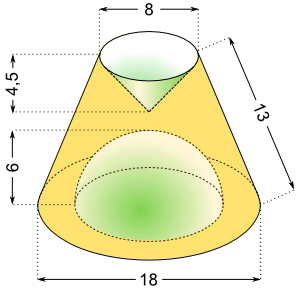 (Maße in cm) |
||||||||||||||||||