Mehrstufige Zufallsversuche 
- Produkt- und Summenregel A 1 - A 6
- Zufallsversuche mit zurücklegen A 7 - A 13
- Zufallsversuche ohne zurücklegen A 14 - A 22
- Gegenereignis A 23 - A 30
- Vierfeldertafel A 31 - A 42
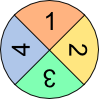
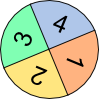
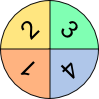
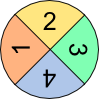
Setzen sich Versuche aus mehreren hintereinander oder gleichzeitig ausgeführten einstufigen Versuchen zusammen, so spricht man von mehrstufigen Versuchen. Die Wahrscheinlichkeit, beim ersten Glücksrad ein A zu drehen liegt bei 1 3 . Die Wahrscheinlichkeit, beim zweiten Glücksrad ein A zu drehen liegt bei 1 6 . Wie hoch aber ist die Wahrscheinlichkeit, gleichzeitig mit beiden ein A zu drehen? Für die Beantwortung dieser Frage ist es hilfreich, mehrstufige Zufallsversuche in einem Baumdiagramm darzustellen. Mit seiner Hilfe lassen sich die unterschiedlichen Wahrscheinlichkeiten berechnen. An jedem Pfad steht die Wahrscheinlichkeit des jeweiligen Ergebnisses. Für die Berechnung der Gesamtwahrscheinlichkeiten gelten dann zwei Regeln:
Produktregel:
Die Wahrscheinlichkeiten entlang eines Pfades werden miteinander multipliziert.
Beispiel: Die Wahrscheinlichkeit, dass die beiden Glücksräder unten je ein A anzeigen (AA) liegt bei 1 3 · 1 6 = 1 18 .Summenregel:
Besteht ein Ereignis aus mehreren Pfaden, dann werden die Einzelwahrscheinlichkeiten dieser Pfade addiert.
Beispiel: Die Wahrscheinlichkeit, dass die beiden Glücksräder zwei gleiche Buchstaben anzeigen (AA oder BB) liegt bei 1 18 + 2 9 = 5 18 .
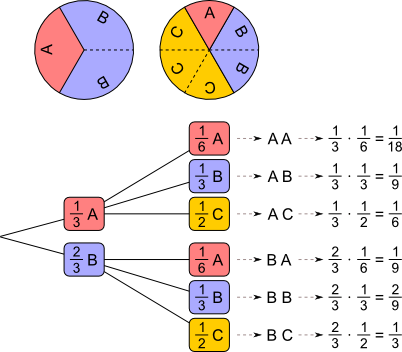
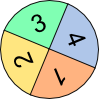
Aufgabe 1: Wie hoch ist die Wahrscheinlichkeit, dass mit den oberen Glücksrädern die Kombination AB oder BC zustande kommt?
| Die Wahrscheinlichkeit, dass eine der beiden Buchstabenfolgen erscheint, liegt bei | . | |
Versuche: 0
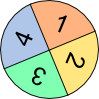
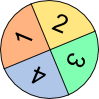
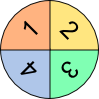
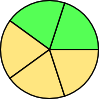
Aufgabe 2: Die zwei Glücksräder drehen sich gleichzeitig. Trage die einzelnen Wahrscheinlichkeiten der Ergebnisse gekürzt in das Baumdiagramm ein.
 |
 |
|||||||
| = grün | ||||||||
| = grün | ||||||||
| = gelb | ||||||||
| |
||||||||
| = grün | ||||||||
| = gelb | ||||||||
| = gelb | ||||||||
richtig: 0falsch: 0
Aufgabe 3: Die Wahrscheinlichkeit, dass bei den oberen Glücksrädern ...
| a) gleichzeitig grün erscheint, liegt bei | . ← Produktregel | ||
| b) gleichzeitig gelb erscheint, liegt bei | . ← Produktregel | ||
| c) mindestens ein Mal grün kommt, ist | . ← Produkt- und Summenregel | ||
| Kürze die Ergebnisse so weit wie möglich! | |||
richtig: 0falsch: 0
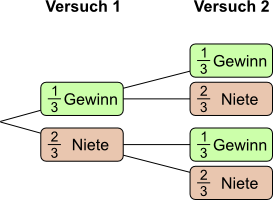
Aufgabe 4: Bei einem Glücksrad gewinnt ein Drittel aller Felder. Wie wahrscheinlich ist es, das bei zweimaligem Drehen kein Gewinn erzielt wird?
| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
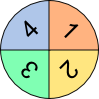
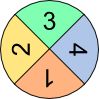
Aufgabe 5: Das Glücksrad wird zwei Mal gedreht. Trage unten die richtigen Wahrscheinlichkeiten für die angegebenen Summen der beiden Glücksradzahlen als gekürzten Bruch und in Prozent ein.
|  |
||||||||
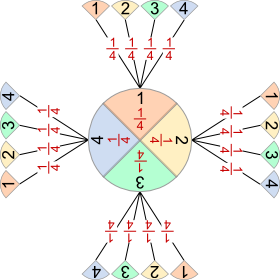| als gekürzter Bruch |
in Prozent |
||||||||
| a) Summe = 5 | % | ||||||||
| b) Summe > 5 | % | ||||||||
| c) Summe ≥ 5 | % | ||||||||
| d) Summe ≠ 5 | % | ||||||||
Versuche: 0
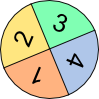
Aufgabe 6: Das Glücksrad wird zwei Mal gedreht. Trage unten die richtigen Wahrscheinlichkeiten für die angegebenen Zahlen als gekürzten Bruch ein.
 |
als gekürzter Bruch |
 |
|||
| a) gleiche Augenzahl | |||||
| b) Augensumme 7 | |||||
| c) Augensumme 5 | |||||
Versuche: 0
Aufgabe 7: Die 3 Glückssymbole Marienkäfer, Kleeblatt und Glückspilz werden vom Computer mit einer Wahrscheinlichkeit von 1 3 angezeigt. Mit welcher Wahrscheinlichkeit erscheinen bei 2 Versuchen hintereinander:
Kürze so weit es geht. |
Versuch 1 |
Versuch 2 |
||||||||||||||
 |
||||||||||||||||
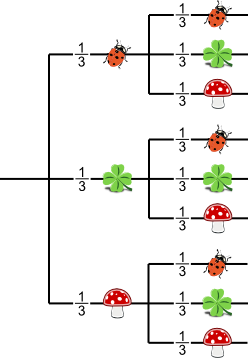Versuche: 0
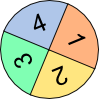
Aufgabe 8: Wie groß ist die Wahrscheinlichkeit mit dem unteren Glücksrad die aufgeführten Buchstabenkombinationen zu erzielen?
 |
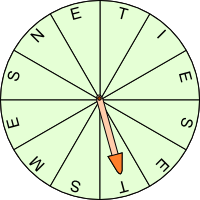E-S | 1 |
| I-S-T | 1 | |
| E-I-N | 1 | |
| E-I-S | 1 | |
| I-M | 1 | |
| T-E-E | 1 | |
Versuche: 0
Aufgabe 9: Das Glücksrad wird zweimal gedreht. Wie groß ist die Wahrscheinlichkeit, eine Summe von höchsten 4 (Summe ≥ 4) zu erhalten?
| Die Wahrscheinlichkeit beträgt | . | |
Versuche: 0
Aufgabe 10: Das Rad wird zweimal gedreht. Bestimme die Wahrscheinlichkeiten für:
| a) | zweimal Grün (A) | 1 |  |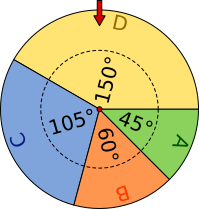
| b) | erst Grün (A), dann Blau (C) | ||
| 192 | |||
| c) | einmal Orange (B), einmal Gelb (D) | ||
| 36 | |||
| d) | genau einmal Blau (C) | ||
| 288 | |||
| e) | höchsten einmal Grün (A) | ||
| 64 | |||
| f) | keinmal orange |
||
| 36 |
Versuche: 0
Aufgabe 11: |
Ein Würfel wird zwei Mal hintereinander geworfen. a) Mit welcher Wahrscheinlichkeit ergibt die Summe der beiden Punkte folgende Ergebnisse? Trage die fehlenden Nenner der Brüche ein.
|
Versuche: 0
Aufgabe 12: Beim "Mensch-ärgere-dich-nicht-Spiel" hat man anfänglich drei Versuche, um eine Sechs zu Würfeln. Wie wahrscheinlich ist es, das mit drei Würfen mindestens ein Mal zu schaffen?
| Die Wahrscheinlichkeit, mindestens ein Mal eine Sechs zu würfeln, liegt bei | . | ||
| 216 |
Versuche: 0
Aufgabe 13: In einem Beutel befinden sich rote, blaue und grüne Kugeln. Nach dem Ziehen einer Kugel, wird ihre Farbe notiert und die Kugel wieder in den Beutel zurückgelegt. Die Wahrscheinlichkeit:
|
Wie groß ist die Wahrscheinlichkeit, zwei grüne Kugeln zu ziehen?
Kürze so weit wie möglich.
| Die Wahrscheinlichkeit, zwei grüne Kugeln zu ziehen, beträgt | . | |
richtig: 0falsch: 0
Aufgabe 14: | Aus dem unteren Sack werden 2 Kugeln nacheinander gezogen. Die zuerst gezogene Kugel wird nicht zurückgelegt. |
|||||
| a) | Wie groß ist die Wahrscheinlichkeit, dass zwei rote Kugeln gezogen werden? | |||||
| b) | Wie groß ist die Wahrscheinlichkeit, dass genau eine blaue Kugel gezogen wird? | |||||
|
Aufgabe von 15 |
||||||
| Antwort: | a) |
|
||||
| b) |
|
|||||
| Kürze die Ergebnisse soweit wie möglich! | ||||||
richtig: 0falsch: 0
Aufgabe 15: In einem Geldbeutel befinden sich die Münzen, die vor dem Diagramm aufgeführt sind. Zwei Münzen werden nacheinander zufällig aus dem Beutel genommen. Ergänze die aufgeführten Wahrscheinlichkeiten.
Münze 1 | Münze 2 | |||||||
 |
|
|||||||
 |
|
|
||||||
|
||||||||
|
|
|||||||
|
|
|||||||
|
||||||||
|
|
|||||||
|
|
|||||||
|
||||||||
richtig: 0falsch: 0
Aufgabe 16: Mit welcher Wahrscheinlichkeit wird aus dem oberen Geldbeutel ...
| a) zwei Mal eine 5 Cent genommen? | . | ||
| b) mindestens ein Mal eine 1 Euro geholt? | . | ||
| Kürze die Ergebnisse so weit wie möglich! | |||
richtig: 0falsch: 0
Aufgabe 17: Sieben deutsche und drei portugiesische Ein-Euro-Münzen liegen in einer Kiste. Nachdem eine Münze mit geschlossenen Augen gezogen wurde, wird sie auf einem Tisch abgelegt. Mit welcher Wahrscheinlichkeit liegt eine portugiesische Münze mit der Zahl nach oben auf dem Tisch?
Die Wahrscheinlichkeit dafür liegt bei %.
Versuche: 0
Aufgabe 18: Ein Multiple-Choice-Test besteht aus drei Aufgaben mit jeweils vier Antworten. Bei jeder Aufgabe ist nur eine Antwort richtig. Wie wahrscheinlich ist es, dass jemand, der die Antworten nicht kennt, durch Zufall a) alle, b) mindestens zwei und c) mindestens eine Antwort richtig hat? Gib die Lösung als gekürzten Bruch an.
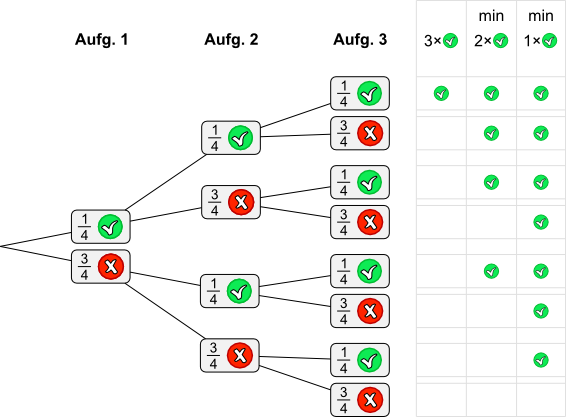
| Antwort: Die Wahrscheinlichkeit | a) alle drei Antworten richtig anzuklicken liegt bei | . | |
| b) mindestens zwei Antworten richtig zu haben ist | . | ||
| c) mindestens eine richtige Antwort zu treffen ist | . | ||
Versuche: 0
Aufgabe 19: Unter zehn Fahrgästen einer Straßenbahn befinden sich zwei Schwarzfahrer. Ein Kontrolleur bittet 3 Personen, ihren Fahrschein vorzuzeigen. Wie groß ist die Wahrscheinlichkeit, dass beide Schwarzfahrer in die Kontrolle geraten?
| Die Wahrscheinlichkeit, beide Schwarzfahrer zu erwischen, liegt bei | 1 |
Versuche: 0
Aufgabe 20: |
Von 6 Karten haben jeweils zwei das gleiche Symbol (2 x Dreieck, 2 x Quadrat, 2 x Kreis). Sie liegen verdeckt auf dem Tisch und du ziehst ohne zu kontrollieren zwei Stück. |
| a) | Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole zu ziehen? |
| b) | Mit welcher Wahrscheinlichkeit ziehst du mindestens einen Kreis? |
| c) | Du ziehst drei Kärtchen. Wie hoch ist die Wahrscheinlichkeit, drei unterschiedliche Symbole zu ziehen? |
| Antwort: a) | Die Wahrscheinlichkeit, zwei gleiche Symbole zu ziehen, liegt bei %. |
| b) | Die Wahrscheinlichkeit, mindestens einen Kreis zu ziehen, liegt bei %. |
| c) | Die Wahrscheinlichkeit, bei drei Zügen drei unterschiedliche Symbole zu ziehen, liegt bei %. |
Versuche: 0
Aufgabe 21: Auf einem Tisch liegen verdeckt 20 Karten. Jede Karte ist mit einem der Buchstaben A, B oder C bedruckt. Auf 2 5 der Karten befindet sich das A und auf 45 % das B. Nacheinander werden zwei Karten ohne zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit, genau eine Karte mit dem Buchstaben C zu ziehen? Trage den fehlenden Zähler ein.
| Die Wahrscheinlichkeit beträgt | . | |
| 190 |
Versuche: 0
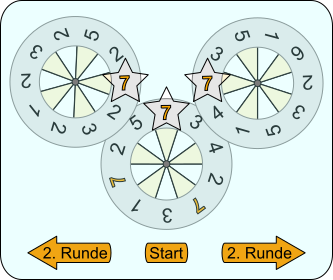
Aufgabe 22: Unten siehst du die Scheiben eines Spielautomaten, bei dem das dreimalige Erscheinen der Zahl 7 in den Sternenfeldern den Hauptgewinn erzielt.
| a) | Wie hoch ist die Wahrscheinlichkeit, dass die 7 in allen drei Sternenfeldern erscheint, wenn der Automat von außen nicht beeinflusst wird? |
| b) | Die linke und die rechte Scheibe können bei nicht Erscheinen der gewünschten Zahl jeweils ein zweites Mal aktiviert werden. Mit welcher Wahrscheinlichkeit erscheint am Ende des Spieles drei Mal die 7, wenn diese Möglichkeit genutzt wird? |
 |
|
|||||||||||||||||||||||||||||||||||
|
||||
|
Versuche: 0
Gegenereignis
Ergebnisse, die als Ereignis bei einem Zufallsversuch erwünscht sind, bezeichnet man als günstige Ereignisse. Ergebnisse, die nicht erwünscht sind, heißen ungünstige Ereignisse. Alle ungünstigen Ereignisse bilden das Gegenereignis.
Beispiel: Am Anfang eines "Mensch-ärgere-Dich-nicht-Spiels" wünscht sich jeder Spieler als Ereignis eine 6. Die Wahrscheinlichkeit, sie zu würfeln, liegt bei 1 6 . Die Wahrscheinlichkeit für ein Gegenereignis (1, 2, 3, 4, 5) liegt bei jedem Wurf bei 5 6 . Rechnerisch bedeutet das:
| P(Ereignis) | = 1 - | P(Gegenereignis) | |
| Beispiel: 1 6 | = 1 - | 5 6 | |
| P(Gegenereignis) | = 1 - | P(Ereignis) | |
| Beispiel: 5 6 | = 1 - | 1 6 | |
Aufgabe 23: Trage unter die Wahrscheinlichkeiten der Ereignisse die Wahrscheinlichkeiten der Gegenereignisse ein.
| Ereignis: |
|
|
% | % | ||||||
| Gegenereignis: |
|
|
% | % |
richtig: 0falsch: 0
Aufgabe 24: Klick das richtige Gegenereignis an.
- Ereignis: Eine Zahl würfeln, die kleiner als 5 ist.
Gegenereignis: Eine Zahl würfeln, die
- Ereignis: Aus einem Beutel mit roten, blauen und gelben Zetteln einen blauen Zettel ziehen.
Gegenereignis: Aus einem Beutel mit roten, blauen und gelben Zetteln
- Ereignis: Aus einem Skatspiel eine Karte zu ziehen, die weder ein Bube noch ein Dame ist.
Gegenereignis: Aus einem Skatspiel eine Karte zu ziehen, die
Versuche: 0
Aufgabe 25: Aus einem Beutel mit 3 blauen und 3 roten Kugeln werden zwei Kugeln gezogen. Mit welcher Wahrscheinlichkeit ist keine rote Kugel dabei.
Mit einer Wahrscheinlichkeit von % ist keine rote Kugel dabei.
Versuche: 0
Aufgabe 26: Aus einem Beutel mit 3 blauen und 3 roten Kugeln werden zwei Kugeln gezogen. Mit welcher Wahrscheinlichkeit ist mindestens eine rote Kugel dabei (Gegenereignis zu Aufgabe 25).
Mit einer Wahrscheinlichkeit von % ist mindestens eine rote Kugel dabei.
Versuche: 0
Aufgabe 27: Berechne die Wahrscheinlichkeit, dass aus einem Schachspiel eine beliebige Figur genommen wird, die kein Pferd ist. Mit Hilfe des Gegenereignisses geht es einfacher. Antwort: Die Wahrscheinlichkeit, dass kein Pferd genommen wird, liegt bei %. Versuche: 0 |
|
Aufgabe 28: Zwei Würfel werden gleichzeitig geworfen. Es ist kein Sechserpasch. Trage die Lösung als gekürzten Bruch ein.
| Die Wahrscheinlichkeit, keinen Sechserpasch zu würfeln, liegt bei | . | |
Versuche: 0
Aufgabe 29: Bei einem Glücksrad gewinnt jedes fünfte Feld. Wie wahrscheinlich ist es, dass bei zweimaligem Drehen kein Gewinn dabei ist?
Die Wahrscheinlichkeit liegt bei %.
Versuche: 0
Aufgabe 30: In einem Sack sind nur eine grüne und eine rote Kugel. Es wird drei Mal gezogen. Die gezogene Kugel wird jedes Mal zurückgelegt. Wie groß ist die Wahrscheinlichkeit, das mindestens ein mal Grün erscheint? Berechne mit Hilfe des Gegenereignisses. Trage den gekürzten Bruch ein.
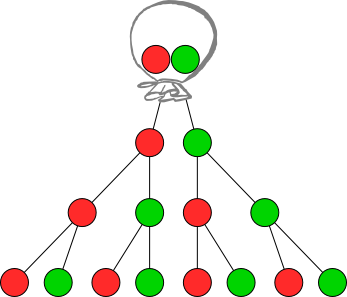
| Die Wahrscheinlichkeit liegt bei | . | |
Versuche: 0
Vierfeldertafel
Eine Vierfeldertafel eignet sich dazu, Mengen darzustellen, die aus zwei Merkmalen mit jeweils zwei Ausprägungen bestehen.
- Beispiel: Die 14 Mädchen und und 11 Jungen einer Klasse werden gefragt, ob die nächste Klassenfahrt an die See oder in die Berge gehen soll. Die Umfrage ist folgendermaßen ausgefallen:
| Merkmal 1 Geschlecht |
|||||
| Klassenfahrt | Ausprägung 1 Mädchen |
Ausprägung 2 Jungen |
|||
| Merkmal 2 Ort |
Ausprägung 1 Berge |
4 | 5 | 9 | Zeilen- summe |
| Ausprägung 2 See |
10 | 6 | 16 | ||
| 14 | 11 | 25 | |||
| Spaltensumme | |||||
Aufgabe 31: In einer Klasse wird festgestellt, wer seine Zunge rollen kann. Trage die fehlenden Werte in die Vierfeldertafel ein.
| Zungenroller | Mädchen | Jungen | |
| ja | |||
| nein | |||
richtig: 0falsch: 0
Aufgabe 32: In einer Klassenstufe wird über einen smartphonefreien Tag abgestimmt. Trage die fehlenden Werte in die Vierfeldertafel ein.
| Smartphonefreier Tag |
Klasse 10 a |
Klasse 10 b |
|
| dafür | % | 20 % | % |
| dagegen | 22 % | % | % |
| % | 52 % | 100 % |
richtig: 0falsch: 0
Aufgabe 33: Von den 36 Rauchern einer 78 Schüler starken 10ten Jahrgangsstufe sind 22 im Sportverein. 32 Jugendliche gehören keinem Sportverein an. Trage die notwendigen Daten in die Vierfeldertafel ein.
| Raucher | Nicht- raucher |
||
| Sportverein | |||
| kein Sportverein | |||
richtig: 0falsch: 0
Aufgabe 34: Von 108 Schülern wünschen sich 74, einmal eigene Kinder groß zu ziehen. 35 % der Jungen möchten allerdings keine Kinder haben. Von den 48 Mädchen ist eine Mehrheit für eigene Kinder. Wie viele Mädchen und wie viele Jungen möchten später einmal eigene Kinder haben?
 |
| Kinderwunsch | Mädchen | Jungen | |
| positiv | |||
| negativ | |||
Später möchten Mädchen und Jungen einmal eigene Kinder haben.
Versuche: 0
Aufgabe 35: Ein neuer Schwangerschaftstest hat in der Erprobung bei 940 Schwangeren ein positives Ergebnis geliefert. 50 Frauen waren nicht schwanger. Insgesamt fiel der Test bei 960 der 1000 untersuchten Frauen positiv aus. Wie viel Prozent der Frauen haben ein falsches Ergebnis präsentiert bekommen?
| Schwanger- schaftstest |
Frau ist schwanger |
Frau ist nicht schwanger |
|
| Test ist positiv |
|||
| Test ist negativ |
|||
Bei % der Frauen zeigte der Test ein falsches Ergebnis an.
Versuche: 0
Aufgabe 36: Besteht ein Zufallsversuch aus zwei Ereignissen, die jeweils eintreten können oder auch nicht, dann kann man zur Auswertung die entsprechenden Wahrscheinlichkeiten ebenfalls in einer Vierfeldertafel anordnen. Unten siehst du den entsprechenden Aufbau in versprachlichter Form. Klick unten jeweils die Zeichen an, die in den roten Rahmen gehören.
| Ereignis B tritt ein |
Ereignis B tritt nicht ein |
||
| Ereignis A tritt ein |
Wahrscheinlichkeit, dass A und B eintreten |
Wahrscheinlichkeit, dass A eintritt und B nicht |
Wahrscheinlichkeit, dass A eintritt |
| Ereignis A tritt nicht ein |
Wahrscheinlichkeit, dass B eintritt und A nicht |
Wahrscheinlichkeit, dass A und B nicht eintreten |
Wahrscheinlichkeit, dass A nicht eintritt |
| Wahrscheinlichkeit, dass B eintritt |
Wahrscheinlichkeit, dass B nicht eintritt |
100 % |
| B | B | gesamt | |
| A | P( ) | P( ) | P( ) |
| A | P( ) | P( ) | P( ) |
| gesamt | P( ) | P( ) | 100 % |
Versuche: 0
Aufgabe 37: 94 % eines neuen Schwangerschaftstests fiel bei Schwangeren positiv aus. 50 Frauen waren nicht schwanger. Insgesamt fiel der Test bei 96% der 1000 untersuchten Frauen positiv aus. Trage die entsprechenden Wahrscheinlichkeiten in die Vierfeldertafel ein (Daten aus Aufgabe 35 in Prozent).
| Schwanger- schaftstest |
Frau ist schwanger |
Frau ist nicht schwanger |
|
| Test ist positiv |
% | % | % |
| Test ist negativ |
% | % | % |
| % | % | 100 % |
Versuche: 0
Aufgabe 38: In zwei Regionen wurde der gleiche Corona-Schnelltest an je 10000 Personen durchgeführt. Er zeigt bei 80 % der Infizierten das richtige Ergebnis an (Sensitivität). Von den nicht Infizierten erhalten 98 % tatsächlich ein negatives Testergebnis (Spezifität).
Insgesamt waren in Astetten 5, im Breichgau 1000 Personen infiziert. Positiv fielen in Astetten 204 und im Breichgau 980 Tests aus. Bei nicht infizierten Personen gab es in Astetten 9795 negative Tests, im Breichgau 8820.
Mit welcher Wahrscheinlichkeit ist jemand in den beiden Regionen tatsächlich infiziert, wenn er ein positives Testergebnis erhält? Runde auf eine Nachkommastelle.
| Astetten | Breichgau | ||||||
| Person ist | gesamt | Person ist | gesamt | ||||
| infiziert | nicht infiziert |
infiziert | nicht infiziert |
||||
| Test ist positiv |
|||||||
| Test ist negativ |
|||||||
| gesamt | 10000 | 10000 | |||||
Die Wahrscheinlichkeit, dass jemand tatsächlich infiziert ist, wenn er ein positives Testergebnis erhält, liegt in Astetten bei % und im Breichgau bei %.
Versuche: 0
Aufgabe 39: Von 1000 Autofahrern verursachen 3 einen Unfall. Einer dieser Unfälle geht auf Alkoholkonsum zurück. 5,1% der Autofahrer sind alkoholisiert. Wie hoch ist jeweils die Wahrscheinlichkeit alkoholisiert bzw. nüchtern einen Unfall zu verursachen? Runde auf eine Nachkommastelle.
| Autofahrer | Unfall- verursacher |
kein Unfall- verursacher |
|
| alkoholisiert | |||
| nüchtern | |||
| 1000 |
Die Wahrscheinlichkeit unter Alkoholeinfluss einen Unfall zu verursachen liegt bei %. Die Wahrscheinlichkeit nüchtern einen Unfall zu verursachen liegt bei %.
Versuche: 0
Aufgabe 40: Ein Uhrhändler erhält 40 Uhren, von denen 65 % mit Tagesanzeige sind. Ein Fünftel der Uhren hat ein Stahlarmband. 12 Uhren haben keine Tagesanzeige und kein Stahlarmband. Wie viele Uhren mit Stahlarmband haben eine Tagesanzeige?
|
| Uhr | Tagesanzeige | keine Tagesanzeige |
|
| Stahlarmband | % | % | % |
| kein Stahlarmband | % | % | % |
| % | % | % |
Von den Uhren mit Stahlarmband haben % eine Tagesanzeige.
Versuche: 0
Aufgabe 41: In der Fangioallee und in der Laudastraße werden Geschwindigkeitskontrollen durchgeführt. Von den 500 Autos in der Fangioallee sind 4 % zu schnell gefahren. Von den 300 Fahrzeugen der Laudastraße waren es 8 %. Bei wie viel Prozent aller Autos wurde eine Tempoüberschreitung festgestellt?
|
| Geschwindigkeits- kontrolle |
Fangio- allee |
Lauda- straße |
|
| Tempo angepasst |
KFZ % |
KFZ % |
KFZ % |
| Tempo zu schnell |
KFZ % |
KFZ % |
KFZ % |
|
500 KFZ % |
300 KFZ % |
800 KFZ 100 % |
Bei % aller Fahrzeuge wurde ein zu hohes Tempo gemessen.
Versuche: 0
Aufgabe 42: In einer Voliere sind 2 5 der Wellensittiche Männchen und 3 5 Weibchen. 75 % der Männchen und 1 6 der Weibchen haben ein blaues Gefieder. Gina beobachtet einen blauen Vogel. Mit welcher Wahrscheinlichkeit handelt es sich um ein Männchen? Trage die richtigen Werte in die Vierfeldertafel und in den Lösungssatz ein.
| Wellensittiche | m | w | gesamt |
 blau |
% | % | % |
 grün |
% | % | % |
| gesamt | % | % | 100 % |
Die Wahrscheinlichkeit, dass Gina ein Männchen betrachtet liegt bei %.
Versuche: 0