Zinsformeln
Zinsen lassen sich mit Hilfe von 4 Formeln berechnen, die folgendes Muster aufweisen.
- Werden die Zinsen gesucht, steht im Nenner der Formel 360 · 100.
Alle übrigen Größen werden im Zähler miteinander multipliziert.
- Werden die Zinsen nicht gesucht, steht im Zähler der Formel Z · 360 · 100.
Alle übrigen Größen, außer der gesuchten Größe, werden im Nenner miteinander multipliziert.
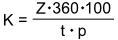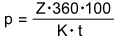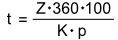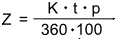
Aufgabe 1: Schiebe die Formelelemente an ihren richtigen Platz.
K = Kapital | p = Zinssatz | t = Verzinsungszeit | Z = Zinsen
| K = |
Z · 360 · 100 | p = | Z · 360 · 100 | Zähler | ||
| t · p | K · t | Nenner | ||||
| t = | Z · 360 · 100 | Z = | K · t ·p | |||
| K · p | 360 · 100 |
Aufgabe 2: Werte die Formeln aus Aufgabe 1 aus und klick die richtigen Antworten an.
1) Auf welche gesuchten Größen trifft zu, dass Z · 360 · 100 im Zähler steht? (K) (p)(t) (!Z)
2) Welche Größe wird gesucht, wenn t · p im Nenner steht? (K) (!p)(!t) (!Z)
3) Welche Größe wird gesucht, wenn K · t im Nenner steht? (!K) (p)(!t) (!Z)
4) Welche Größe wird gesucht, wenn K · p im Nenner steht? (!K) (!p)(t) (!Z)
5) Welche Größe wird gesucht, wenn 360 · 100 im Nenner steht? (!K) (!p)(!t) (Z)
Aufgabe 3: Ordne zu, welche Größen gesucht werden, wenn die angegebenen Terme im Zähler, beziehungsweise im Nenner stehen.
| Zähler: Z · 360 · 100 | Kapital | Zinssatz | Verzinsungszeit |
| Nenner: 360 · 100 | Zinsen |

